Foundations of Analysis

Lecture 1: Holes in the rational numbers.

Much of the subject of real analysis is motivated by physics. Over the years,
scientists have constructed many models of the physical world which predict its
behavior with increasing accuracy. In the classical models, space and time are
represented as a continuum, rather than as a bunch of tiny pixels packed in some
multi-dimensional arrangement. The notion we have of the continuum is very intu-
itive to the human brain. However, constructing the continuum in a way which is
precise, useful and well organized involves a large degree of abstraction. One needs
to pin down the abstract mathematical properties of the continuum and investigate
how these relate to each other.

The main point of our task is to construct or at least characterize the real line.
To do this we start with the set of rational numbers m/n where m and n are integers
with n ≠ 0. (Of course we identify m/n with (cm)/(cn) for c ≠ 0.

Ordered Sets. Let S be a set. An order on S is a relation denoted by < with the
following two properties.
(i) If x ∈ S and y ∈ S then exactly one of the following three statements is true:

x < y, x = y, y < x.

(ii) If x, y, z ∈ S and x < y and y < z then x < z.

Remark. We write x ≤ y to mean "x < y or x = y", etc..

The rationals are ordered are arranged in a straight line by the ordering

p < q 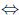q - p is positive:

Note that a positive rational is one which can be written as m/n where m and n
have the same sign. For a rational number p, either p is positive or p is zero or - p
is positive.

The reason that the rationals do not satisfy our intuitive picture of a continuum
is that they are riddled with holes.

Theorem. There is no rational number whose square is 2.

Proof. Suppose that there exists a rational a/b such that (a/b)² = 2. Then by
dividing a and b by a power of 2, we can assume that 2 does not divide both a and
b. Now we have a² = 2b², so a² is even and hence a is even. (To see that the square
of an odd number is odd, we notice that (2k + 1)² = 2(2k² + 2k) + 1.) But then
4|a² = 2b², and 2|b², so b² is even, so b is even which is a contradiction.

Definition. Let

A = {p : p > 0, p is rational and p² < 2}.

Let

B = {p : p > 0, p is rational and p² > 2}.

For example, some elements of A are given by terms in the decimal expansion of

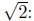
1, 1.4, 1.41, 1.414, 1.4142, …

Theorem. A contains no largest element and B contains no smallest element.

Proof. We show that for each p ∈ A we can find q ∈ A with q > p. How should
we choose q? We have p² < 2 and want q = p + α rational with (p + α)² < 2. But
if α < 1 then

(p +α)² = p² + 2pα + α² < p² + (2p + 1)α.

But we can indeed choose α so that the right hand side is less than 2. Indeed,

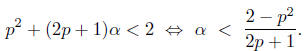
Similarly for the claim on B.

Remark. More generally it can be shown that if n is not a square number, then
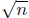is irrational. The facts that are needed to prove this general fact are given
below.

We are going to write down the properties which characterize the real numbers.
Many texts on the subject actually construct the rational numbers from the integers
and then construct the real numbers from the rational numbers in a mathematically
rigorous way. We are not going to do this, only because it takes some time. However,
the student who is interested should take a look at the appendix to Chapter 1 of
the book.

Supremum and Infimum. Suppose that S is an ordered set, and E 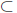S.
We say that β ∈ S is an upper bound for E if x ≤ β for every x ∈ E.
We say that E is bounded above if there exists β ∈ S which is an upper bound for
E.
We say that β ∈ S is the least upper bound or supremum of E if β is an upper
bound for E, and if α < β, then α is not an upper bound for E.

Example. S is the rationals. Consider the following subsets E of the rationals:

(1). E = {p : p > 0; p² < 1}.
2 is an upper bound. 1 is the supremum. 1 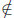E.

(2). E = {p : p > 0; p² ≤1}.
2 is an upper bound. 1 is the supremum. 1 ∈ E.

(3). E = {p : p > 0}.
E is not bounded above.

(4). E = A = {p : p > 0; p² < 2}.

2 is an upper bound. There is no supremum for E in S.

Similarly, suppose that S is an ordered set, and E 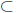S.
We say that β ∈ S is a lower bound for E if β ≤ x for every x ∈ E.
We say that E is bounded below if there exists β ∈ S which is a lower bound for E.
We say that β ∈ S is the greatest lower bound or infimum of E if β is a lower bound
for E, and if β < α, then α is not a lower bound for E.

Least Upper Bound Property. An ordered set is said to have the least upper
bound property if: Whenever 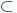E S is non-empty and bounded above, then the
supremum of E exists in S.

We saw that the rationals do not have the least upper bound property.

Appendix: Elementary number theory facts you can use to show that 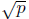is irra-
tional if p is prime.

Factorization of integers. In this appendix, Z denotes the integers and Z⁺
denotes the positive integers.

If n, d ∈ Z, and n = cd for some c ∈ Z, we say d is a divisor of n or n is a
multiple of d. We write d|n. The integer n > 1 is called prime if its only positive
divisors are 1 and n. Using the principal of induction, one can show that every
integer n > 1 can be represented as a product of prime factors in only one way,
apart from the order of the factors. This is known as the Fundamental Theorem of
Arithmetic. For our purposes right now, we just want the following:

Theorem 1.8 If a prime p divides ab then p|a or p|b. More generally if a prime p
divides 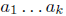then it divides at least one of the factors.

Clearly we only need to show this for a and b positive. For a and b in Z⁺, we
denote by (a, b) the largest positive integer which divides both a and b.

Theorem 1.6 If a, b ∈ Z⁺ have (a, b) = 1, then we can find integers x and y with

1 = ax + by:

Proof. By induction. If a = b = 1 then this is trivial because

1 = 1 · 1 + 1 · 0.

We will carry out induction on the maximum of a and b. Assume the statement
has been proven when this maximum is at most n ≥ 1, and now consider the case
when the maximum equals n + 1. Without loss of generality assume a ≤ b. We
only have something to prove in the case (a, b) = 1, and since b > 1 this implies
that a < b. (Else a = b and (a, b) = b > 1.) Hence 1 ≤ a ≤ b. But the maximum of
a and b - a is less than b. Moreover, (a, b - a) = (a, b) = 1. Hence by induction,

1 = ax + (b - a)y,

for some integers x and y. But then

1 = a(x - y) + by.

By induction, we have proved the result.

Now we can complete the proof of Theorem 1.8. Indeed, if p|ab but p does not
divide a, then (a, p) = 1, so we can find integers x and y with

1 = ax + py:

But then

b = abx + pby

and p divides the right hand side so p|b.

The value d is called the greatest common divisor of a and b and is denoted by
(a, b). Any other common divisor of a and b must divide it.