Math 20A Final Review Outline
Chapter 3: Differentiation
Section 3.1: Definition of the Derivative
• Know what is meant by the difference quotient
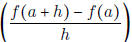 , it is the the slope of the
, it is the the slope of the
secant line through the points (a, f(a)) and (a + h, f(a + h))
• Know the definition of the derivative at a point x = a and how it relates to
the difference
quotient. The formula is 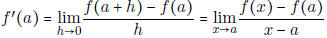
- If f(x) = (x + 1)2 − 2, find f'(0) using the definition of the derivative.
- Let 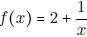 . Find f'(3) using only the definition of the derivative.
. Find f'(3) using only the definition of the derivative.
- Suppose f(x) is a function such that f(3) = 1 and f(3 + h) − f(3) = h2 + heh.
(i) Find f'(3) (ii) Find an equation for the tangent line to the graph of y = f(x) at x = 3.
- The line y = 3x + 5 is tangent to the graph of f at the point (1,8). (i) Find
f(1) and (ii)
Find f'(1).
| • Know that the derivative at a point is the slope of the tangent
line to the curve at that point. - The slope, m, of the tangent line of y = x2 at x = 1 is 2. Visually, we have the picture to the right. • Know how to find the tangent line to a graph at a point. - Find the equation of the tangent line of y = x2 at (1,1). - If f is differentiable on (−∞,∞), f(0) = 5, and f'(x) ≥ 3, how small can f(4) possibly be? |
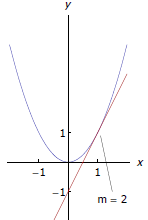 |
• Know how to use the difference quotient to estimate the derivative at a
point (use small values
of h)
| • Know how to order various slopes - In the figure to the right, list the following quantities in increas- ing order: 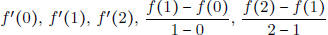 . . |
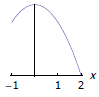 |
Section 3.2: The Derivative as a Function
• Know the definition of the derivative (as a function). That is,
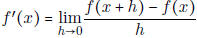
• Know how to recognize some limits are just being derivatives in disguise
- Notice that 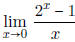 is just the derivative of 2x
at
x = 0.
is just the derivative of 2x
at
x = 0.
• Know the different types of notation used for the derivative of y = f(x): (i)
y', (ii) y'(x), (iii)
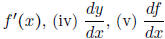
• Know the different types of notation used for the derivative of y = f(x) at a
point x = a: (i)
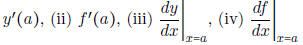
• Know what the derivative tells us graphically:
 If f'(x) > 0 on an interval, then f(x) is increasing over that interval.
If f'(x) > 0 on an interval, then f(x) is increasing over that interval.
 If f'(x) < 0 on an interval, then f(x) is decreasing over that interval.
If f'(x) < 0 on an interval, then f(x) is decreasing over that interval.
• Note: Just because f(x) is increasing does not mean that f'(x) is increasing.
It only means
that f'(x) > 0. It is easy to confuse the two.
• Know the power rule for taking derivatives: 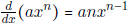 ,
where a is a constant and n
,
where a is a constant and n
is any number.
- Find the derivative of f(x) = x5 + 4x3 + 27.
• As a special case of the above, if f(x) = c (a constant), then f'(x) = 0 for
all x.
• Another special case of the power rule is
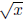 .
.
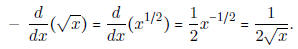
• Note: The power rule only applies to the case where the variable (usually x)
is raised to a
power. It is not true that the derivative of y = 3x is y'(x) =
x3x-1!
• Know that f(x) may have a local max/min wherever f'(x)
= 0.
• If you have a constant times a function that you are taking the derivative of,
you can factor
out the constant.
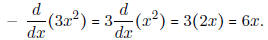
• If you are taking the derivative of the sum/difference of two functions, you
can take the
derivative of each piece
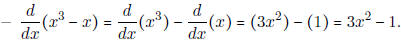
• Know that the derivative of y = bx is proportional to bx. (In fact, we see
in Section 3.10 that
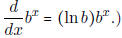
• Know that the derivative of y = ex is ex.
• Know the relationship between derivatives and continuity.
• If a function is differentiable, then it is continuous. The converse is not
necessarily true!
- The function y = lxl is continuous, but not differentiable at x = 0. (Using the
definition
of the derivative, we see that f'(0) does not exist since the limit from the
left does not
equal the limit from the right.)
• So, that means that if f(x) is not continuous at x = a, then f(x) is not
differentiable at x = a.
• f(x) is not differentiable at any sharp point, i.e. where we can t more than
one tangent line
• f(x) is not differentiable wherever the function has a vertical slope
Section 3.3: The Product and Quotient Rules
• Know the product and quotient rules and how to apply them to solve problems.
 Product Rule:
Product Rule: 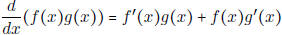 .
.
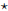 Quotient Rule:
Quotient Rule: 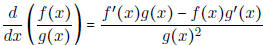 .
.
• To remember the Quotient Rule, use the song "low-d-high minus high-d-low
over low squared
and away we go"
• Note: The derivative of fg is not equal to f'g' and the derivative of f/g is
not equal to
f'/g'
- Find the derivative of (i) x2(x3 + 1) using the product rule (ii)
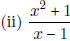 and (iii)
and (iii) 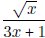 .
.
Section 3.4: Rates of Change
• Know how that the derivative is the instanteous rate of change (often just
mentioned as
ROC).
• Know that the rate dy/dx is measured in "units of y per unit of x".
• For motion, velocity v(t) is the ROC of position s(t) with respect to time.
That is, s'(t) = v(t).
Acceleration a(t) is the ROC of velocity v(t) with respect to time. That is,
v'(t) = a(t).
• 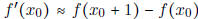 , so
, so
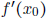 can be a good estimate of the change in f
due to a
can be a good estimate of the change in f
due to a
one-unit change in x, when 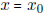 .
.
- Marginal cost is the cost of producing one additional unit. If C(x) is the
cost of producing
x units, then the marginal cost at production level
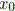 is
is 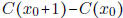 . The
derivative
. The
derivative
C'(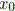 ) is then a good estimate for the marginal cost.
) is then a good estimate for the marginal cost.
• Know Galileo's formulas for the height and velocity at time t of an object
rising and valling
under the influence of gravity near the earth's surface
- 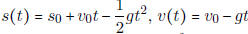 , where
, where 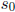 = initial position,
= initial position,
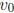 = initial velocity, and
= initial velocity, and
g is the constant 9.8m/s2 or 32ft/s2.
- The acceleration of an object falling due to gravity is 32ft2/sec on the
surface of the
Earth. An object is thrown upward from the surface of the Earth at an initial
speed of
64 ft/sec. How high does the object go, and how long does it take to reach that
height?
Section 3.5: Higher Derivatives
• Know what the second derivative tells us about f(x) and f'(x).
 If f''(x) > 0, then f'(x) is increasing and f(x) is concave up.
If f''(x) > 0, then f'(x) is increasing and f(x) is concave up.
 If f''(x) < 0, then f'(x) is decreasing and f(x) is concave down.
If f''(x) < 0, then f'(x) is decreasing and f(x) is concave down.
• The following table should help to keep the relationships straight
| The graph of f(x) | Sign of f'(x) | Sign of f''(x) |
| Increasing, concave up | Positive | Positive |
| Increasing, concave down | Positive | Negative |
| Decreasing, concave up | Negative | Positive |
| Decreasing, concave down | Negative | Negative |
• Know that f(x) may change concavity wherever f''(x)
= 0.
• Note: f''(x) is the derivative of f'(x). So, the same properties that we
discussed for the rst
derivative apply to these two functions.
• Given the graph of f'(x), know where f(x) is increasing/decreasing, concave
up/down
- Let 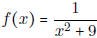 . Compute f''(x). On what interval(s)
is f(x) concave down?
. Compute f''(x). On what interval(s)
is f(x) concave down?
- Let f(x) = x2ex. Where is f(x) increasing? Where is f(x) concave down?
- Find the values of a and b such that (1, 6) is a point of inflection for the
curve y =
x3 + ax2 + bx + 1.
- Let f(x) = 3x5 − 20x3. (i) Find all x-intercepts and y-intercepts of the graph
of f. (ii)
Determine the interval(s) where f is increasing and the interval(s) where f is
decreasing.
(iii) Find all local extrema of f, and determine which are local maxima and
which are
local minima. (iv) Determine the interval(s) where the graph of f is concave up
and the
interval(s) where the graph of f is concave down. (v) Find the point(s) of inflection of
the graph of f.
• Know that higher derivatives are defined by successive differentiation. That is,
the third
derivative of f(x) is found by taking the derivative of f''(x).
• Returning to the equations of motion from the previous section, we have that
s'(t) = v(t) and
since v'(t) = a(t), we have that s''(t) = a(t).


