MATH 511 ASSIGNMENT SHEET

We hope to cover most of the text, and in particular give full attention to some
interesting applications. This sheet will be updated throughout the semester, and I
may make some remarks on several of the homework problems.

The course will move fast, and it is important to come to every class. The
book is written in a very informal way, and unless you read it very critically you
will have difficulty understanding what the author is saying, my job is partly to
help you in this. The author has good summaries in the text, but you might slide
over them --- read carefully.

Some of the homework problems have answers/solutions in the back. There are
far too many problems for us to penetrate a good percentage, but there are lots of
opportunities for you to work out problems on your own.

I plan at least one major exam and either one or two more big exams or else
several quizzes, likely every Friday, a program of many quizzes may help the class
keep to date.

We will learn soon that matrix multiplication is not commutative. So we will usually
think of vectors as row vectors, and so usually write Ax for the action of A on the
vector x. That means that rows and columns will play different roles.

1.1-1.3 Systems of Linear Equations. This introduces the basic framework and
reinforces the value of a geometric viewpoint, as well as simply computing. From
high school we learn that n `linear' equations in n unknowns `has' one and only one
solution, but in fact this is not always true | it depends on how you count! We
view such a system as either n linear equations with real numbers unknown or as a
single equation in n-dimensional vectors. We introduce Gaussian elimination and
address the efficiency of this algorithm. Problems: p. 9: 2, 3 4, p. 15: 6, 11, 18.

1.4 Matrices and their algebra. Matrices are an efficient may to express systems
of equations in a way to which humans can relate. Elementary matrices provide an
algebraic way to interpret Gaussian elimination. Problems: p. 26: 2, 3(a), 7, 20,
24

1.5 Triangular factorization. Decomposition A = LU or (more symmetrically)
A = LDU (p. 36) if there are no row exchanges necessary. Otherwise, need to ap-
ply principle to PA instead of A, where P is a permutation matrix, and P^-1 = P^T :
Problems: p. 39: 1, 5, 6, 8, 13.

1.6 Inverses, symmetric matrices. Problems: p. 52: 5, 6, 11 (a, b), 13.
Review: p. 65: 12, 19, 22.

2.1 Vector spaces (subspaces). Closed under + and scalar multiplication. This
is where you should be clear on the definition: some strange objects can be vec-
tor spaces. Contrast subspace and subset. Two important subspaces arise in
solving systems of linear equations: the nullspace and the column space, be sure
that you can make clear sentences about solving linear equations in terms of these
(sub)spaces. Problems: p. 73: 2, 3, 7 (a, b, c).

2.2 Ax = b in the general case. Echelon, row(-reduced) echelon form, pivot and
free variables. Note procedures outlined informally on pp. 80 and 83. Problems:
p. 85: 2, 4, 6, 11.

2.3 Linear independence, basis, dimension. Problems: p. 98: 1, 6, 18, 19.

2.4 Fundamental (sub)spaces of an (m n) matrix A. Column space (dim r),
nullspace (dim n−r), row space (sol space of A^T ), left nullspace (nullspace of A^T ).
(The first two are in R^m, the other two in Rⁿ.) These are related to the echelon
forms U and (reduced echelon) R of A. The fundamental theorem of linear algebra
is on p. 106. We learn about left/right inverses. Problems: p. 110: 3, 4, 7, 11, p.
137: 2, 5.

2.6 Linear Transformations. Definition: T (cx+dy) = cT(x)+dT(y): Examples
come from matrix algebra and also from `function spaces,' operations such as f →
f',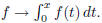 Determined by action on a basis (however, (x+y)² ≠ x² +y²!).
Special matrices: P (projection), Q (rotation), H (reflection). Problems: p. 133:
4, 6, 7, p. 137: 29. 31.

3.1 Lengths, Angles, Orthogonality Orthogonal complements. Fundamen-
tal theorem of orthogonality (p. 144). Reinterpret fundamental theorem of linear
algebra. Problems: p. 148: 2, 3, 11, 14, 19.

3.2 Cosine! is more important than sin : Projection onto a subspace (high-school
math helps here). Projection: P² = P. Note: sometimes I write (x, y) instead of
xy^T (which the book uses). Problems: p. 157: 3, 5, 10, 12, 17.

3.3 Least squares. Find `best' solution to Ax = b with b confined to a subspace
S. If e(⊂ S) is this solution so that 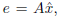then e is perpendicular to S. The
number of applications of this section is a course in itself, we just skim the surface.
Problems: p. 170: 3, 4 (think about why calculus is relevant here!), 22, 23, 31.

3.4 Orthogonal matrices and bases. (Book notes that `orthonormal' matrix
would be a better term.) If Q is orthogonal and square! then Q^-1 = Q^T . Q is
reserved for matrices with orthonormal rows. If Q is square, every vector
may be written as a linear combination of the rows of Q, and we get a formula for
the coefficients: if 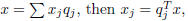where 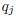is the jth row of Q.

If Q is not square (so it will ' ! have to ! have more rows than columns), then
we want the best (least-squares) solution to Qx = b. The Gram{Schmidt process
transforms any linearly independent set of vectors into an equivalent (what do we
mean by that?) set of othonormal vectors. Problems: p. 185: 1, 3, 6, 11.

3.4' Now factor a matrix A as A = QR; Q is orthogonal and R is right-triangular
(not quite the U we had in Chapter 1), and R is invertible.
We apply these ideas to vector spaces of functions and see that expanding a
function in a Fourier series is just the Gramm-Schmidt process. (Don't be terrified
by this, it just uses the formulas we've been developing.) Best linear t for data.
Problems: p. 187, 16, 21, 25, 29.
End of Chapter 3 for us.

4.1 -4.3 Determinants. We follow the text and define the deerminant of an
n × n matrix A, det(A) or |A|, as a function of A which is 1 for the identity matrix,
changes sign when two rows are interchanged (this is a special kind of permutation
called a transposition), and is linear with respect to operations on the first row.

Of course, this has many consequences, which are points 3{10 in x4.1 of the
book. Be a little careful (!), since sometimes people learn a formula for the 3 × 3
determinant which doesn't work when n > 3. We derive several formulas for |A|,
including the one with cofactors. In principle, det(A) involves nⁿ sums, but we see
quickly that there are really only n! sums (which is far less than nⁿ).
Problems: p. 206: 5, 8, 15, 17(c), 28, 29, p. 215: 5, 6, 9 (a, b), 12 (challenging).

4.4 Applications of determinants. Formula for A^-1 (not computationally e -
cient), Cramer's rule. Determinants and volumes. We answer the question directly
now: when does A factor: A = LU?
Problems: 3, 5, 10, 14, 15, 28.
End of Chapter 4

5.1 Introduction to eigenvalues. Instead of Ax = 0, we now ask: when does the
equation 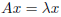(where 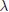is a scalar) have a nontrivial solution (so that x ≠ 0).
This comes up in systems of equations, and we quickly find that for most there
is only the trivial solution. The x for which this euqation has a solution are called
eignevectors , and our goal is to find, as best as possible, a basis consisting only
of eigenvectors (why is this a good idea?). The trace and determinant of A are
expressed in terms of the eigenvalues of A. Does a nontrivial rotation have any
eigenvectors?

Problems: p. 240: 3, 4, 7, , 11, 14, 25, 26 [which is why we will be introducing
complesx number fairly soon], 30.

5.2 Best case: diagonalization. If there are n linearly independent eigenvectors,
then A can be diagonalized with respect to a basis consisting of eigenvectors.

The matrix S with eigenvactors as columns is said to effiect a similarity. Eigen-
vectors corresponding to di erent eigenvalues are linearly independent.
Problems: p. 250: 4, 5, 12, 17, 24 29, 30.

5.4 e^A and stability. If we can diagonalize 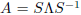, then du/dt = Au has
the solution 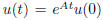, and this is very easy to compute. The solutions are
stable if < i < 0 for all i, and unstable when at least one has positive real part.

We show how a linear equation of higher order may be written as a first-order
linear system.

Problems: p. 275: 1, 3, 7, 14 [use material at bottom of p. 273 as model], 21,
22, 36.

5.5 Complex matrices. Material to p. 282 bottom is routine. New vocabu-
lary: Hermetian, unitary matrix (analogues of symmetric and othrogonal matri-
ces). Good dictionary on p. 288. The famous spectral theorem is introduced in an
o hand manner on p. 285.

Problems: 7, 8(!), 11, 14, 20.

Appendix B (Jordan form). Here we sketch what happens when the matrix A
cannot be diagonalized, the Jordan form is the best we can do.

Problems: p. 427: 1(b), 6, 7.

5.6 Similarity as a subject in itself. We think of a similarity matrix as express-
ing a change of basis (usually made so that a linear transformation is simpler to
understand with respect to a different basis). We can always transform a matirx
A by a unitary similarity U^-1AU to be triangular (what happens if A is Herme-
tian??). Spectral theorem formally stated on p. 297. Examples for Jordan form.
p. 298: Normal matrices defined: these are exactly the matrices with a full set of
orthonormal eignevectors.

Problems: p. 302: 3, 5, 8, 9, 12, 15, 18, 20, 24, 35 [also find e^J ], 38, 41.

3.5 FFT Very efficient, one of the most quoted papers on the last century.

Problems: p. 196: 1, 3, 7, 11, 15, 18, 21 [don't try this if not comfortable].
Positive Definite Matrics. Saddle points.

6.1 (review of MA 261!, can be done via quadratic formula.) Consider the
quadratic form x^T Ax { is it always positive? Can it change signs?? This is the
second term of a Taylor series.
Problems. p. 316: 3, 4, 7, 9, 15, 20.

6.2 Tests for P. D.
Problems. p. 326: 1, 4, 7, 10, 17, 29//

6.3: `[a] great matrix factorization.' Any matrix A may be factored as A =
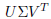where the outside factors are square. The columns of U, V come from
eigenvalues of AA^T,A^TA. we touch upon some applications.
Problems. 1, 2, 6, 8, 10, 14.

6.4 Minimum principles. Most of this only is for positive definite matrices. We
get the formula for least squares (see p. 162)

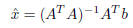
in another manner. We also consider the Rayliegh quotient

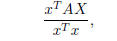
which is easy to analyse with respect to an orthogonal basis (which is always pos-
sible!).
Problems. 1, 2, 5, 7, 11a.

7.2 Matrix norm, sensitivity. We define the `norm' of the matrix A as
||A||= max|Ax|,

where the maximum is over vectors x of length 1. This can be written other ways.
It is easy to compute for p. d. matrices, in general we replace a not-necessarily-
=p. d. matrix A by A^TA or AA^T , but must remember to take square roots. The
condition number of a p. d. matrix is max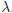 / min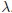 , and we show that this relates
to errors in computation.
Problems. p. 357: 1, 5, 6, 11a, 12 bc, 13 a.