Mathematics Content Expectations
| Form A: Math Alignment Table | |||||
| Alignment to Math High School Content Expectations | |||||
| Math High School Content Expectations | Prealgebra Math 050 to Summer 2006 |
Prealgebra Math 050 to Fall 2006 |
Introductory Algebra Math 107 Summer and Fall 2006 |
Math 112 | ACCUPLACER Tests |
| STANDARD G2: RELATIONSHIPS BETWEEN FIGURES Students use and justify relationships between lines, angles, area and volume formulas, and 2- and 3-dimensional representations. They solve problems and provide proofs about congruence and similarity. |
|||||
| G2.1 Relationships Between Area and Volume Formulas |
|||||
| G2.1.1 Know and demonstrate the relationships between the area formula of a triangle, the area formula of a parallelogram, and the area formula of a trapezoid. |
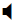 |
||||
| G2.1.2 Know and demonstrate the relationships between the area formulas of various quadrilaterals (e.g., explain how to find the area of a trapezoid based on the areas of parallelograms and triangles). |
|||||
| G2.1.3 Know and use the relationship between the volumes of pyramids and prisms (of equal base and height) and cones and cylinders (of equal base and height). |
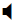 |
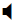 |
|||
| G2.2 Relationships Between Two-dimensional and Three-dimensional Representations |
|||||
| G2.2.1 Identify or sketch a possible
3-dimensional figure, given 2-dimensional views (e.g., nets, multiple views); create a 2-dimensional representation of a 3- dimensional figure. |
|||||
| G2.2.2 Identify or sketch cross-sections of 3- dimensional figures; identify or sketch solids formed by revolving 2-dimensional figures around lines. |
|||||
| G2.3 Congruence and Similarity | |||||
| G2.3.1 Prove that triangles are congruent using
the SSS, SAS, ASA, and AAS criteria, and for right triangles, the hypotenuse-leg criterion. |
|||||
| G2.3.2 Use theorems about congruent triangles to prove additional theorems and solve problems, with and without use of coordinates. |
|||||
| G2.3.3 Prove that triangles are similar by using
SSS, SAS, and AA conditions for similarity. |
|||||
| G2.3.4 Use theorems about similar triangles to
solve problems with and without use of coordinates. |
|||||
| G2.3.5 Know and apply the theorem stating that
the effect of a scale factor of k relating one two dimensional figure to another or one three dimensional figure to another, on the length, area, and volume of the figures is to multiply each by k, k2, and k3, respectively. |
|||||
| STANDARD G3: TRANSFORMATIONS OF FIGURES IN THE PLANE Students will solve problems about distance-preserving transformations and shape-preserving transformations. The transformations will be described synthetically and, in simple cases, by analytic expressions in coordinates. |
|||||
| G3.1 Distance-preserving Transformations: Isometries |
|||||
| G3.1.1 Define reflection, rotation, translation,
and glide reflection and find the image of a figure under a given isometry. |
|||||
| G3.1.2 Given two figures that are images of each other under an isometry, find the isometry and describe it completely. |
|||||
| G3.1.3 Find the image of a figure under the composition of two or more isometries, and determine whether the resulting figure is a reflection, rotation, translation, or glide reflection image of the original figure. |
|||||
| G3.2 Shape-preserving Transformations: Dilations and Isometries |
|||||
| G3.2.1 Know the definition of dilation, and find
the image of a figure under a given dilation. |
|||||
| G3.2.2 Given two figures that are images of each other under some dilation, identify the center and magnitude of the dilation. |
|||||
| RECOMMENDED: | |||||
| *G1.4.5 Understand the definition of a cyclic quadrilateral, and know and use the basic properties of cyclic quadrilaterals. |
|||||
| *G1.7.4 Know and use the relationship between the vertices and foci in an ellipse, the vertices and foci in a hyperbola, and the directrix and focus in a parabola; interpret these relationships in applied contexts. |
|||||
| *G3.2.3 Find the image of a figure under the composition of a dilation and an isometry. |
|||||
| STRAND 4: STATISTICS AND PROBABILITY (S) | |||||
| In Kindergarten through Grade 8,
students develop the ability to read, analyze, and construct a
repertoire of statistical graphs. Students also examine the fundamentals of experimental and theoretical probability in informal ways. The Basic Counting Principle and tree diagrams serve as tools to solve simple counting problems in these grades. During high school, students build on that foundation. They develop the data interpretation and decision-making skills that will serve them in their further study of mathematics as well as in their coursework in the physical, biological, and social sciences. Students learn important skills related to the collection, display, and interpretation of both univariate and bivariate data. They understand basic sampling methods and apply principles of effective data analysis and data presentation. These skills are also highly valuable outside of school, both in the workplace and in day-to-day life. In probability, students utilize probability models to calculate probabilities and make decisions. The normal distribution and its properties are studied. Students then use their understanding of probability to make decisions, solve problems, and determine whether or not statements about probabilities of events are reasonable. Students use technology when appropriate, including spreadsheets. This strong background in statistics and probability will enable students to be savvy decision-makers and smart information-consumers and producers who have a full range of tools in order to make wise choices. |
|||||


