More on Equivalence Relations

1.1 quadratic polynomials

Let Q be the set of all real quadratic polynomials. That is .

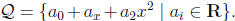Define a relation T on Q as follows:

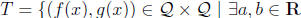with a ≠ 0 and f(ax + b) = g(x)} .

Exercise 1.1 Let f(x) = x² and g(x) = x² + x. Is (f(x), g(x)) ∈ T? That is, do there
exist real numbers a, b with a ≠ 0 such that (ax + b)² = x² + x? Show that the answer is
no.
Hint: If so (this is a proof by contradiction), then there exist real numbers a, b with a ≠ 0
such that

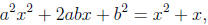
which implies (by comparing the coefficients) that a² =?, 2ab =?, and b² = 0. Why is this
impossible?

Exercise 1.2 Now let’s start with a different pair of quadratics, f(x) = x² and g(x) =
4x² + 4x + 1. Show that (f(x), g(x))∈ T: Again we seek real numbers a, b such that

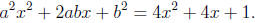
Find a solution.

Exercise 1.3 Prove that T is an equivalence relation.

Hint: Here is a proof that the relation ~ is symmetric. (You should show that T is
reflexive and transitive.) Suppose that (f(x), g(x)) ∈ T, that is,

f(ax + b) = g(x), (1)

for some real numbers a ≠ 0 and b. To prove that (g(x), f(x)) ∈ T we need to show that

g(cx + d) = f(x), (2)

for some real numbers c ≠ 0 and d.

Actually we can compute and express c and d in terms of a and b. Here’s how it works.
Let c, d be any real numbers and substitute cx + d for x in Equation (1):



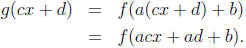
By choosing c = 1/a and d = -b/a, we have acx + ad + b = x so that g(cx + d) = f(x).
Thus c = 1/a and d = -b/a are the real numbers that make Equation (2) true.

Since this is an equivalence relation we will drop the use of T and the ordered pairs and
simply write f(x) ~ g(x) to mean (f(x), g(x)) ∈ T.

There are two natural questions that arise in this context. Given two quadratics, how can
we tell if they are equivalent? Is there a set of “simple” quadratics such that every other
quadratic is congruent to one of these?

We try to tackle the first question first. A fairly simple observation will help here. Suppose
f(x) = Ax² + Bx + C and g(x) = Dx² + Ex + F are quadratics and that f(x) ~ g(x).
Then the leading coefficients A,D have the same sign. That is, A and D are either both
positive or both negative. To see this, suppose that a, b are real numbers with a ≠ 0 and
f(ax + b) = g(x). Then compute

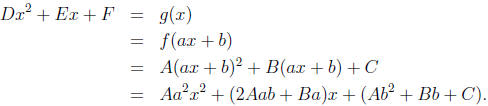
Thus D = Aa²and so A and D have the same sign. To state this observation in a more
symbolic way, let sgn(f(x)) denote the sign of the leading coefficient of f(x). That is,
sgn(f(x)) = +1 if the leading coefficient is positive and sgn(f(x)) = -1 if the leading
coefficient is negative. The observation proved above can be stated in the following way:

Theorem 1.4 Let f(x), g(x) be quadratic polynomials. If f(x) ~ g(x) then sgn(f(x)) =
sgn(g(x)).

The function sgn is called an invariant of the equivalence relation. (We will give a more
general definition later.) This invariant is useful because it allows us to prove that certain
quadratics are not equivalent. For example, f(x) = 2x² + 3x + 4 is not equivalent to
g(x) = -5x² + 7x - 9 because sgn(f(x)) = +1 and sgn(g(x)) = -1. Thus using the
contrapositive form of Theorem 1.4, we know that

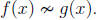
Unfortunately, the converse of Theorem 1.4 does not hold. The quadratics f(x) =
x², g(x) = x²+x discussed above provide a counterexample. sgn(f(x)) = sgn(g(x)) = +1,
but f(x) is not equivalent to g(x). However there is another invariant which when combined
with the sign invariant will provide necessary and sufficient conditions for equivalent.
More on this later.

Exercise 1.5 Find a counterexample to this statement: If f(x) = Ax² + Bx + C and
g(x) = Dx² + Ex + F and f(x) ~ g(x) then C and F have the same sign.

1.2 invariants and reduced forms

Let’s pause now to explain what an invariant is and what a reduced form is for a general
equivalence relation.

Definition 1.6 Let ~ be an equivalence relation on a set A. A function
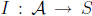
from A onto a set S is an invariant for the equivalence relation if x~ y implies that
I(x) = I(y) for all x, y ∈ A.

Now suppose that I is an invariant. Sometimes we can use I to determine that two
elements x, y ∈ A are not equivalent. That is, if I(x) ≠ I(y) then 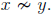On the other
hand, it may happen that I(x) = I(y) but for some x, y ∈ A.

Definition 1.7 Let ~ be an equivalence relation on a set A and let 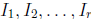  be invariants
for the equivalence relation. The set of invariants 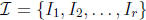is sufficient
if the following property holds:

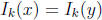  for all k = 1, . . . , r implies x ~y.

A sufficient set of invariants gives us a way to determine if two given elements x, y ∈ A
are equivalent. If 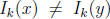for any one of the invariants, then But if
  for all k = 1, . . . , r then x ~ y. Unfortunately we do not have a sufficient
set of invariants our equivalence relation. The function sgn(f(x)) is an invariant for the
equivalence relation on the set of quadratics Q But sgn alone is not a sufficient set of
invariants. Later we will add one other invariant, I, which will make {sgn, I} a sufficient
set of invariants.

Now we turn to the idea of a reduced form for an equivalence relation.

Definition 1.8 Let ~be an equivalence relation on a set A. A subset 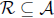is a reduced
subset if every x ∈ A is equivalent to exactly one element of R.

In addition, and this is where the word “reduced” comes in, we would like the elements
in the reduced set R is be simple in some sense.

1.3 A reduced form for quadratic polynomials

Let’s start with an example.

Exercise 1.9 Let g(x) = -x² + 6x + 1. Is g(x) equivalent to a quadratic of the form
-x² + D, where D is a real number? (We are hoping that this will be our reduced form.)
To restate the question in terms of the definition of the equivalence relation, we ask: do
there exist real numbers a ≠ 0, b and D such that -(ax + b)² + D = -x² + 6x + 1?
Hint: By expanding (ax+b)², the question becomes this: do there exist real numbers a ≠ 0,
b, and D such that

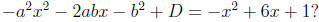
Solve for a, b, and D by comparing coefficients and fill
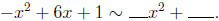
Here’s what we are getting at: The quadratics of the form ±x² + D are fairly simple.
Could it be that every quadratic is equivalent to one of this form? The answer is yes.

Theorem 1.10 Let f(x) be a quadratic polynomial in Q. Then there exists a real number
D such that either f(x) ~ x² + D or f(x) ~ -x² + D.

Exercise 1.11 Prove Theorem 1.10. Hints: Let f(x) = Ax² + Bx + C. Divide the proof
into two cases, A > 0,A < 0. Then complete the square.

Exercise 1.12 Write an explicit expression for the D in terms of A, B, C. The graph of
the quadratic f(x) is a parabola. What is the geometric meaning of D. Is D an invariant?