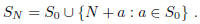NUMBER THEORY
2006-A-3. Let 1, 2, 3, · · · , 2005, 2006, 2007,
2009, 2012, 2016, · · · be a sequence defined by xk = k for
k = 1, 2, · · · , 2006 and
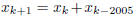for k
≥ 2006. Show that the sequence
has 2005 consecutive terms
each divisible by 2006.
2005-A-1. Show that every positive integer is a sum of one or more numbers of
the form
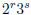, where
r and s are nonnegative integers and no summand divides another. (For example,
23 = 9 + 8 + 6.)
2005-B-2. Find all positive integers n,
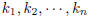such that
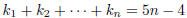and
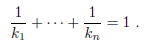
2005-B-4. For positive integers m and n, let f(m, n) denote the number of n−tuples
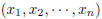
of integers such that
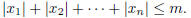Show that f(m, n) = f(n,m).
2004-A-1. Basketball star Shanille O’Keal’s team statistician keeps track of the
number, S(N), of
successful free throws she has made in her first N attempts of the season. Early
in the season, S(N) as
less than 80% of N, but by the end of the season, S(N) was more than 80% of N.
Was there necessarily a
moment in between when S(N) was exactly 80% of N?
2004-A-3. Define a sequence
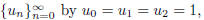and thereafter by the condition that
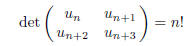
for all n ≥ 0. Show that un is an integer for all n. (By convention, 0! = 1.)
2004-B-2. Let m and n be positive integers. Show that
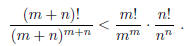
2004-B-6. Let A be a non-empty set of positive integers, and let N(x) denote the
number of elements
of A not exceeding x. Let B denote the set of positive integers b that can be
written in the form b = a − a'
with 
and 
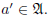. Let
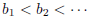be the members of B, listed in
increasing order. Show that if the
sequence
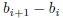is unbounded, then
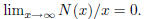
2003-A-1. Let n be a fixed positive integer. How many ways are there to write n
as a sum of positive
integers,
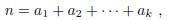
with k an arbitrary positive integer, and
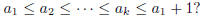For example,
with n = 4, there are
four ways: 4, 2+2, 1+1+2, 1+1+1+1.
2003-A-6. For a set S of nonnegative integers, let
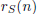denote the number of
ordered pairs (s1, s2)
such that s1 ∈ S, s2 ∈ S, s1
≠ s2, and s1 + s2 = n. Is it possible to partition
the nonnegative integers into
two sets A and B in such a way that
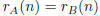for all n?
2003-B-2. Let n be a positive integer. Starting
with the sequence
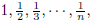for a new sequence
of n − 1 entries
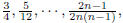by taking the averages of two consecutive entries in the first
sequence.
Repeat the averaging of neighbours on the second sequence to obtain a sequence
of n−2 entries and continue
until the final sequence consists of a single number xn. Show that xn < 2/n.
2003-B-3. Show that for each positive integer n,
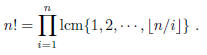
(Here lcm denotes the least common multiple, and [x] denotes the greatest
integer ≤ x.)
2003-B-4. Let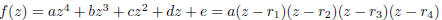
where a, b, c, d, e are
integers, a ≠ 0. Show that if r1 + r2 is a rational number, and if
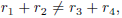then r1r2 is a rational
number.
2002-A-3. Let n ≥ 2 be an integer and Tn be the number of non-empty subsets S of
{1, 2, 3, · · · , n}
with the property that the average of the elements of S is an integer. Prove
that Tn − n is always even.
2002-A-5. Define a sequence by
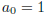, together with the rules
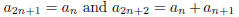for
each integer n ≥ 0. Prove that every positive rational number appears in the set
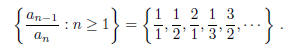
2002-A-6. Fix an integer b ≥ 2. Let f(1) = 1, and f(2) = 2, and for each n
≥ 3,
define f(n) = nf(d),
where d is the number of base−b digits of n. For which values of b does
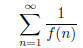
converge?
2002-B-5. A palindrome in base b is a positive integer whose base−b digits read
the same forwards
and backward; for example, 2002 is a 4-digits palindrome in base 10. Note that
200 is not a palindrome in
base 10, but it is the 3-digit palindrome 242 in base 9, and 404 in base 7.
Prove that there is an integer
which is a 3-digit palindrome in base b for at least 2002 different values of b.
2001-A-5. Prove that there are unique positive integers a, n such that
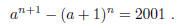
2001-B-1. Let n be an even positive integer. Write the numbers 1, 2, · · · , n2
in the squares of an n×n
grid so that the kth row, from right to left is
(k − 1)n + 1, (k − 1)n + 2, · · · , (k − 1)n + n .
Colour the squares of the grid so that half the squares in each row and in each
column are red and the other
half are black (a checkerboard colouring is one psosibility). Prove that for
each such colouring, the sum of
the numbers on the red squares is equal to the sum of the numbers in the black
square.
2001-B-3. For any positive integer n let
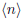denote the closest integer to
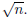Evaluate
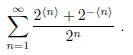
2001-B-4. Let S denote the set of rational numbers different from −1, 0 and 1.
Define f : S → S by
f(x) = x − (1/x). Prove or disprove that
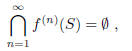
where
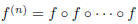(n times). (Note: f(S) denotes the set of all values
f(s) for s ∈ S,)
2000-A-2. Prove that there exist infinitely many integers n such that n, n + 1,
and n + 2 are each the
sum of two squares of integers. (Example: 0 = 02 + 02, 1 = 02 + 12, and 2 = 12 +
12.)
2000-B-1. Let aj , bj , and cj be integers for 1
≤ j ≤ N. Assume, for each j, that
at least one of aj , bj ,
cj is odd. Show that there exist integers r, s, t such that raj + sbj + tcj is
odd for at least 4N/7 values of j,
1 ≤ j ≤ N.
2000-B-2. Prove that the expression
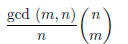
is an integer for all pairs of integers n ≥ m ≥ 1. [Here
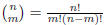and gcd (m, n) is the greatest common
divisor of m and n.]
2000-B-5. Let
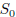be a finite set of positive integers. We define sets
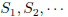of positive integers as
follows:
Integer a is in
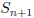if and only if exactly one of a − 1 or a is in Sn.
Show that there exists infinitely many integers N for which
