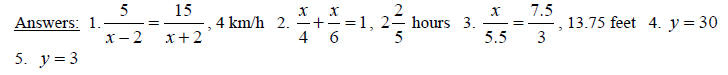Rational Expressions and Their Simplification

Mini Lecture 8.1
Rational Expressions and Their Simplification

Learning Objectives:
1. Find numbers for which a rational expression is undefined.
2. Simplify rational expressions.
3. Solve applied problems involving rational expressions.

Examples:
Find all the numbers for which the rational expression is undefined. If the rational expression is
defined for all real numbers, so state.

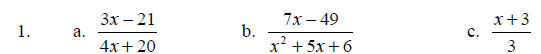
Simplify.

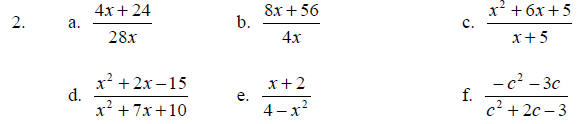
3. The rational expression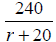describes the time, in hours, to travel 240 miles at a rate of
(r +20) miles per hour.
a. Determine the value of r that would cause the expression to be undefined.
b. Find the time in hours if r = 40.

Teaching Notes:
• Rational expressions are quotients of two polynomials. They indicate division and
division by zero is undefined. We must always exclude any value(s) of the variable that
make a denominator zero.
• When simplifying rational expressions, first, factor the numerator and denominator
completely, then divide both the numerator and the denominator by any common factors.
A rational expression is simplified if its numerator and denominator have no common
factors other than 1 and –1.
• When reducing rational expressions, only factors, not common terms, that are common to
the entire numerator and the entire denominator can be divided out.

Answers: 1. a. x = –5 b. x = –3 and x = –2 c. defined for all real numbers

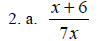
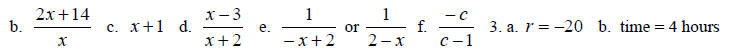
Mini Lecture 8.2
Multiplying and Dividing Rational Expressions

Learning Objectives:
1. Multiply rational expressions.
2. Divide rational expressions.

Examples:
Multiply as indicated.

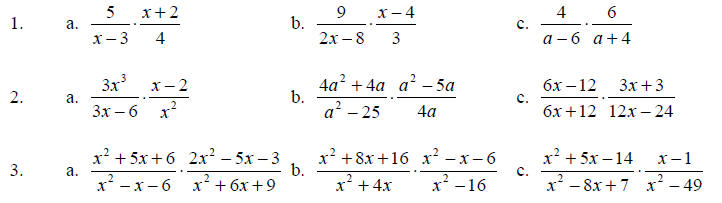
Divide as indicated.

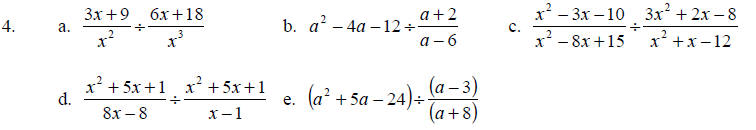
Teaching Notes:
• “When in doubt, factor it out.” Factor first – before multiplying.
• Remind students that in order to divide fractions, (in this section, rational expressions) you
must multiply by the reciprocal of the divisor.

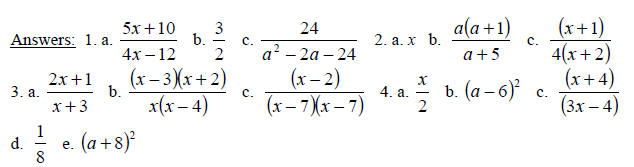
Mini Lecture 8.3
Adding and Subtracting Rational Expressions with the Same Denominator

Learning Objectives:
1. Add rational expressions with the same denominator.
2. Subtract rational expressions with the same denominator.
3. Add and subtract rational expressions with opposite denominators.

Examples:
Add. Simplify if possible.

Subtract, simplify if possible.

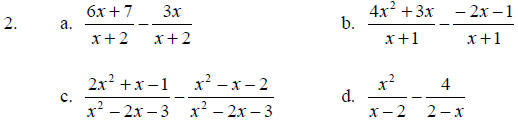
Add, making sure to find a common denominator first and simplify if possible.

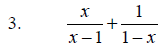
Teaching Notes:
• To add rational expressions with the same denominator, add numerators and place and
sum over the common denominator. Simplify the answer if possible.
• To subtract rational expressions with the same denominator, subtract numerators and
place the difference over the common denominator. Simplify the answer if possible.
• When subtracting numerators with a common denominator, make sure to subtract every
term in that expression.
• When one denominator is the additive inverse of the other, first multiply either rational
expressions by–1/–1 to obtain a common denominator.

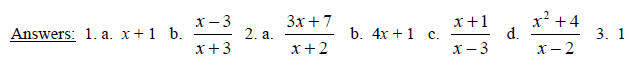
Mini Lecture 8.4
Adding and Subtracting Rational Expressions with Different Denominators

Learning Objectives:
1. Find the least common denominator (LCD).
2. Add and subtract rational expressions with different denominators.

Examples:
Find the least common denominator for the rational numbers or rational expressions. Factor the
denominators first, then build the least common denominator from those factors.

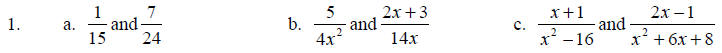
Rewrite each of the following as an equivalent expression with the given denominator.

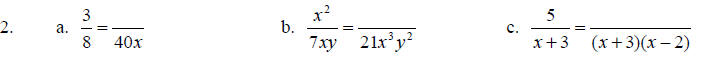
Add or subtract.

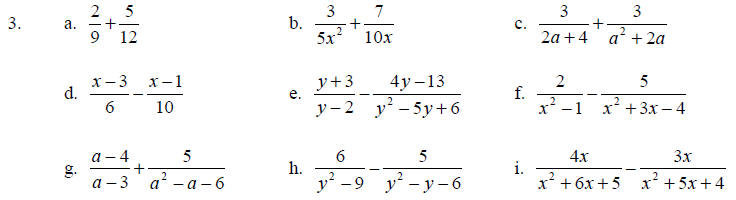
Teaching Notes:
• Students may need to be reminded of factoring steps. It is very important to be able to
factor quickly and completely.
• Students will find this concept easy if they can relate adding and subtracting rational
expressions to adding and subtracting fractions.
• Watch the signs when subtracting!
• Students need to understand that the LCD is build with the factors of the denominators.

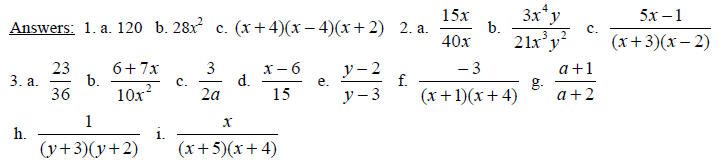
Mini Lecture 8.5
Complex Rational Expressions

Learning Objectives:
1. Simplify complex rational expressions by dividing.
2. Simplify complex rational expressions by multiplying by the LCD.

Examples:
Simplify by dividing; simplify, if possible.

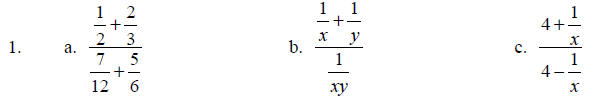
Simplify by the LCD method; simplify, if possible.

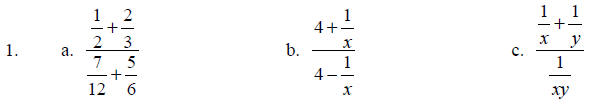
Teaching Notes:
• Complex rational expressions are called complex fractions. They have numerators or
denominators containing one or more rational expressions.
• One method for simplifying a complex rational expression is to combine its numerator
into a single expression and combine its denominator into a single expression, then divide
by multiplying by the reciprocal of the term in the denominator.
• A second method for simplifying a complex rational expression is to multiply each term
in the numerator and denominator by the least common denominator (LCD). This will
produce an equivalent expression that does not contain fractions in the numerator or
denominator.
• Both methods for simplifying complex rational expressions produce the same answer.
See which method you prefer.

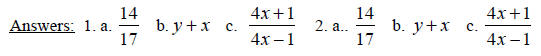
Mini Lecture 8.6
Solving Rational Equations

Learning Objectives:
1. Solve rational equations.
2. Solve problems involving formulas with rational expressions.

Examples:
What is the LCD in each problem?

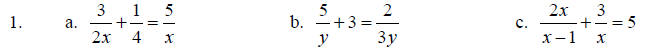
Solve. Clear each equation of fractions first.

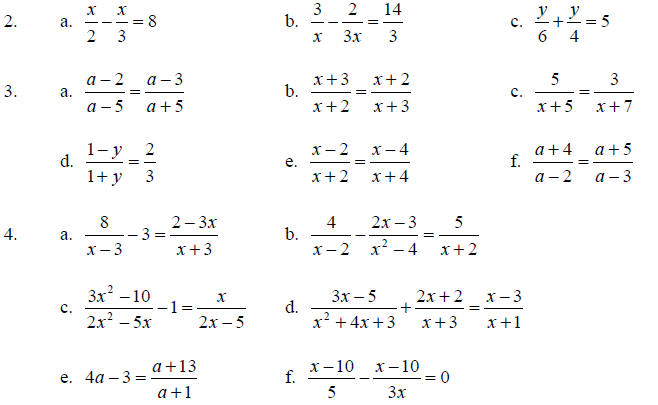
Teaching Notes:
• Students may need extra practice finding the LCD and may need to be reminded to Factor
First.
• When all denominators are in factored form – list the restricted values. Restricted values
is any numbers that would make any denominator zero.
• Some rational equations can be solved using cross products, but students need to be
aware that the method can only be used when there is only one rational expression on
each side of the equation.
• Students need to constantly be reminded to multiply each term or expression on both
sides of the equation by the LCD to get ride of the fractions.
• Students must check solutions for restricted values.

Mini Lecture 8.7
Applications Using Rational Equations and Variation

Learning Objectives:
1. Solve problems involving motion.
2. Solve problems involving work.
3. Solve problems involving similar triangles.
4. Solve problems involving variation.

Examples:
1. A boat travels 5 km upstream in the same amount of time that the boat covers 15 km
downstream. The current in the stream moves at a speed of 2 km/h. What is the speed of the boat
in still water?
2. John working alone can paint a room in 4 hours. His helper, Luke, would need 6 hours to
do the job by himself. If they work together, how long will the paint job take to complete?
3. A tree casts a shadow of 7.5 ft. At the same time, Elizabeth measures the length of her
shadow which is 3 ft. If Elizabeth is 5.5 feet tall, how tall is the tree?
4. If y varies directly as x and y = 200 when x is 300, find y when x = 45.
5. If y varies indirectly as x and y = 42 when x = 50, find y when x = 700.

Teaching Notes:
• Time in motion equation: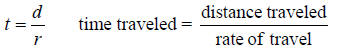
• Work problem equation:

• Similar Figures:
Corresponding angles have the same measure and the ratios of the lengths of the
corresponding sides are equal. In corresponding figures, the lengths of the corresponding
sides are proportional. When triangles ABC and DEF are all similar then:

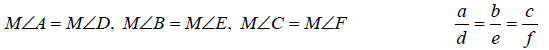
• Direct Variation Equation: y = kx
Where k is the constant of variation, we say that y varies directly as x.
• Inverse Variation Equation: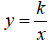
Where k is the constant of variation, we say that y varies indirectly as x.
• With variation questions, write the equation from the English statements. Solve for k and
then substitute the value of k back into the original equation to answer the original
question.