Solving Linear Equations in One Variable
5 Combining Like Terms and Simplifying
Linear equations typically will not be given in standard form and thus will
require some additional preliminary
steps. These additional steps are to first simplify the expressions on each side
of the equal sign using the
order of operations.
5.1 Opposite Side Like Terms
Given a linear equation in the form ax + b = cx + d we must combine like
terms on opposite sides of the
equal sign. To do this we will use the addition or subtraction property of
equality to combine like terms on
either side of the equation.
Example 10
Solve for y: -2y + 3 = 5y + 17
| -2y + 3 = 5y + 17 | |
| -2y + 3 - 5y = 5y + 17 - 5y | Subtract 5y on both sides. |
| -7y + 3 = 17 | |
| -7y + 3 - 3 = 17 - 3 | Subtract 3 on both sides. |
| -7y = 14 | |
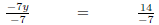 |
Divide both sides by -7. |
| y = -2 |
The solution set is
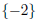 .
.
5.2 Same Side Like Terms
We will often encounter linear equations where the expressions on each side of
the equal sign could be
simplified. If this is the case then it is usually best to simplify each side
first. After which we then use the
properties of equality to combine opposite side like terms.
Example 11
Solve for a:-4a + 2 - a = 3 + 5a - 2
| -4a + 2 - a = 3 + 5a - 2 | Add same side like terms first. |
| -5a + 2 = 5a + 1 | |
| -5a + 2 - 5a = 5a + 1 - 5a | Subtract 5a from both sides. |
| -10a + 2 = 1 | |
| -10a + 2 - 2 = 1 - 2 | Subtract 2 from both sides. |
| -10a = -1 | |
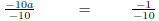 |
Divide both sides by -10. |
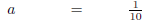 |
The solution set is
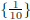 .
.
5.3 Simplifying Expressions First
When solving linear equations the goal is to determine what value, if any, will
solve the equation. A general
guideline is to use the order of operations to simplify the expressions on both
sides first.
Example 12
Solve for x: 5 (3x + 2) - 2 = -2 (1 - 7x)
| 5 (3x + 2) - 2 = -2 (1 - 7x) | Distribute. |
| 5 (3x + 2) - 2 = -2 (1 - 7x) | Add same side like terms. |
| 15x + 10 - 2 = -2 + 14x | |
| 15x + 8 = -2 + 14x | |
| 15x + 8 - 14x = -2 + 14x - 14x | Subtract 14x on both sides. |
| x + 8 = -2 | |
| x + 8 - 8 = -2 - 8 | Subtract 8 on both sides. |
| x = -10 |
The solution set is
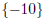 .
.
Figure 2: Video Example 02
6 Conditional Equations, Identities, and Contradictions
There are three different kinds of equations defined as follows.
Definition 3: Conditional Equation
A conditional equation is true for particular values of the variable.
Definition 4: Identity
An identity is an equation that is true for all possible values of the variable.
For example, x = x
has a solution set consisting of all real numbers,
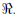 .
.
Definition 5: Contradiction
A contradiction is an equation that is never true and thus has no solutions. For
example, x + 1 =
x has no solution. No solution can be expressed as the empty set f
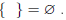
So far we have seen only conditional linear equations which had one value in the
solution set. If when
solving an equation and the end result is an identity, like say 0 = 0, then any
value will solve the equation.
If when solving an equation the end result is a contradiction, like say 0 = 1,
then there is no solution.
Example 13
Solve for x:4 (x + 5) + 6 = 2 (2x + 3)
| 4 (x + 5) + 6 = 2 (2x + 3) | Distribute |
| 4x + 20 + 6 = 4x + 6 | Add same side like terms. |
| 4x + 26 = 4x + 6 | |
| 4x + 26 - 4x = 4x + 6 - 4x | Subtract 4x on both sides. |
| 26 = 6 | False |
There is no solution,
![]() .
.
Example 14
Solve for y:3 (3y + 5) + 5 = 10 (y + 2) - y
| 3 (3y + 5) + 5 = 10 (y + 2) - y | Distribute |
| 9y + 15 + 5 = 10y + 20 - y | Add same side like terms. |
| 9y + 20 = 9y + 20 | |
| 9y + 20 - 20 = 9y + 20 - 20 | Subtract 20 on both sides. |
| 9y = 9y | |
| 9y - 9y = 9y - 9y | Subtract 9y on both sides. |
| 0 = 0 | True |
The equation is an identity, the solution set consists of
all real numbers, ![]() .
.
7 Linear Literal Equations
Literal equations, or formulas, usually have more than one variable. Since the
letters are placeholders for
values, the steps for solving them are the same. Use the properties of equality
to isolate the indicated
variable.
Example 15
Solve for a: P = 2a + b
| P = 2a + b | |
| P - b = 2a + b - b | Subtract b on both sides. |
| P - b = 2a | |
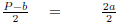 |
Divide both sides by 2. |
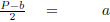 |
Solution:
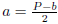
Example 16
Solve for x: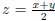
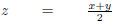 |
|
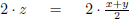 |
Multiply both sides by 2. |
| 2z = x + y | |
| 2z - y = x + y - y | Subtract y on both sides. |
| 2z - y = x |
Solution x = 2z - y
8 Exercises
8.1 Checking Solutions
| Exercise 1 Is x = 7 a solution to - 3x + 5 = -16? |
(Solution on p. 12.) |
| Exercise 2 Is x = 2 a solution to - 2x - 7 = 28? |
(Solution on p. 12.) |
| Exercise 3 Is x = -3 a solution to 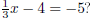 |
(Solution on p. 12.) |
| Exercise 4 Is x = -2 a solution to 3x - 5 = -2x - 15? |
(Solution on p. 12.) |
| Exercise 5 Is x = -1/2 a solution to 3 (2x + 1) = -4x - 3? |
(Solution on p. 12.) |
8.2 Solving in One Step
| Exercise 6 Solve for x: x - 5 = -8 |
(Solution on p. 12.) |
| Exercise 7 Solve for y: - 4 + y = -9 |
(Solution on p. 12.) |
| Exercise 8 Solve for x: 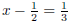 |
(Solution on p. 12.) |
| Exercise 9 Solve for x: 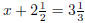 |
(Solution on p. 12.) |
| Exercise 10 Solve for x: 4x = -44 |
(Solution on p. 12.) |
| Exercise 11 Solve for a: - 3a = -30 |
(Solution on p. 12.) |
| Exercise 12 Solve for y: 27 = 9y |
(Solution on p. 12.) |
| Exercise 13 Solve for x: 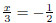 |
(Solution on p. 12.) |
| Exercise 14 Solve for t: 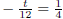 |
(Solution on p. 12.) |
| Exercise 15 Solve for x: 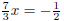 |
(Solution on p. 12.) |