Study Guide for Math 101 Chapter 3

Section 3.5 Geometric and Scientific Applications
Read section 3.5, pages 161 – 168 and answer the following questions as you
read:

1. Describe in your own words what the perimeter of an object or shape
is.

2. Describe in your own words what the area of an object or shape is.

3. Describe in your own words what the volume of an object or shape is.

4. If we want to find the area of a rectangular room and measure the
length to be 15 feet and the width to be 12 feet, what is the area of
the room? What units describe the area?

5. The volume of a right circular cylinder is 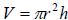. Find the volume of
a right circular cylinder that has a radius of 4 feet an a height of 6
feet. Draw a right circular cylinder and write the units of
measurement for your answer.

6. Use algebra to rewrite the equation with F alone on one side of the
equal sign.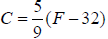

7. Write the formula for simple interest and write what each letter
represents.

8. What is the relationship between distance, rate, and time?

9. Refer to example 5 to answer the questions.

a. How do you find the total cost of 15 pounds of peanuts that
cost $4 per pound? Write the expression that represents the
total cost of 15 pounds of peanuts.

b. How do you find the total cost of x pounds of cashews that cost
$7 per pound? Find an expression for the total cost of x pounds
of cashews.

c. How much do x pounds of cashews and 15 pounds of peanuts
weight when they are mixed together?

d. How do you find the total cost of x + 15 pounds of mixed nuts
that cost $4 per pound?

e. Finish solving the problem and compare your work to the work in
the example. Does the answer make sense?

Section 3.6 Linear Inequalities
Read section 3.6, pages 174 – 182 and answer the following questions as you
read:

1. What is a linear inequality in one variable? How is it different from a
linear equation in one variable?

2. What does it mean to solve an inequality?

3. Why do we graph solution sets of inequalities?

4. Give an inequality that could have the solution set graphed below.
Label three points on the number line that correspond to solutions.

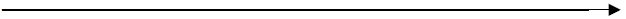
5. Which properties of inequalities are the same as the properties of
equality?

6. Which properties of inequalities are different from the properties of
equality? How are they different?

7. Write the words that you say when you read {x|x < 4}. What is this
notation called?

8. When do you reverse the inequality symbol? Why does this work?

9. How can you check your solutions after you solve an inequality?

10. What is a compound inequality?

11. What type of compound inequality can be written as a double
inequality?

12. Give three numbers that satisfy x<3 and x>2. Graph the solution set.
Write it in set-notation.

13. Give three numbers that satisfy x<3 or x>15. Graph the solution set.
Write it in set-notation.

14. Write an inequality for the statement: x is at most 17.

Section 3.7 Absolute Value Equations and Inequalities
Read section 3.7, pages 186 – 189 and answer the following questions as you
read:

1. What does |x|=3 mean?

2. What are the solutions to |y|=7? Explain.

3. Write the two linear equations equivalent to |x|=12.

4. Write the two linear equations that are equivalent to 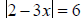, then
solve the equations.

5. Write an absolute value equation that has no solution. Make up a
different one than the ones in the reading. Explain why your equation
has no solution.

6. What must be done first in example 3 before the absolute value is
written as two equations without absolute value symbols? How will you
know when to take this step?

7. Rewrite each of the following absolute value inequalities as a
compound inequality. If the statement can also be written as a double
inequality, write the equivalent double inequality.

Absolute value inequality	Compound inequality	Double inequality (if possible)

8. Do Discussing the Concept in the blue box at the bottom of page 189.
In general, which absolute value inequalities and equations do not have
solutions?

9. What is the midpoint of the interval shown on the number line below?
All of the points in the interval are at most what distance from the
midpoint. Use your answers to write an absolute value inequality that
represents the interval.

10. What skills in this section are new to you and which are skills you
learned in previous sections?

Chapter 3 Review
For each of the following equations
a. What kind of equation or inequality is it?
b. What is your goal?
c. What is your first step?
d. Solve it.
e. Check it.

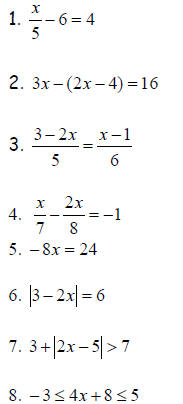
Chapter 3 Practice Test
1. Convert 63.5% to a fraction in simplest form.
2. Convert 6% to a decimal.
3. What number is 235% of 75?
4. When Rod bought his $6000 car, the salesman offered him a 7%
discount, or $500 off. Which is the better deal? Show work.
5. Fay received a wholesale shipment of roses for Valentine’s Day. She
paid $1.12 for each rose. If she sells the roses for $2.25 each, find
the markup. Then, find the percent of markup, rounded to the nearest
hundredth of a percent.
6. In Mrs. Adams’ class, 25 out of 31 students passed their first math
test. In Mr. Brown’s class, 28 out of 34 passed their first math test.
Mr. Brown claimed both classes did equally well. Is he right? If he is
wrong, whose class did better? Show work.
7. Solve the following proportions.

8. A 28-oz jar of peanut butter sells for $4.49.
a. Find the unit price, rounded to the nearest cent. Use
appropriate units in stating your answer.
b. If the unit price remained the same, how much would a 32-oz
jar of peanut butter cost? Express your answer using appropriate units.
9. Jim found that after working for 9 months he had earned 6 days of
vacation time. How many days per year does he earn at this rate?
Identify a variable. Write an algebraic equation. Solve the equation.
10. Solve for t in the following formula: .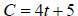
11. A fruit drink is made by mixing fruit juices. An apple juice cocktail
that is 50% juice is to be mixed with a grape juice cocktail that is
30% juice to get 200 liters of a mixture that is 45% juice. How much
of each should be used? Identify a variable. Write an algebraic
equation. Solve the equation.
12. Samantha and Tony operate a small laundry. Samantha, working alone,
can clean a day’s laundry in 9 hours. Tony can clean a day’s laundry in 8
hours. Approximately how long would it take them if they work together?