Written Dialog for Problem Solving
Find an example of a four-term polynomial that cannot be
factored by grouping but can
still be factored.
Is there a pair of rational numbers whose sum and product
are integers but the numbers them-
selves are not?
The Writing Assignment:
Attempt to solve the problem(s) and write about what you tried.
Contrasting writing assignments:
Write a math autobiography.
Why is division by zero undefined?
Write an essay applying a fair division scheme to a real-life problem from your
own experience. The first draft is worth 30% of the grade, the final draft is
70%.
Some Methods of Minimal Guidance
Constructive Approaches:
• Calculus & Mathematica
• ACE/ISETL/APOS
Problem-Solving Approaches
• Ross Summer Program
• Emerging Scholars Programs
Revised Statement of Problem 1
Is there a four-term polynomial that is not prime, does
not have a non-trivial monomial
factor, and cannot be factored by the “factoring by grouping” method?
Part of the dialog is refining the problem.
Some Student Responses
• Guess a polynomial and try to factor
• Attempt to construct by multiplying binomials
Some Instructor Responses
• Try guessing the factored form
• Try all ways of grouping
Promoting Deeper Learning
What is a counter-example?
unique factorization (constructing the example)
playing devil’s advocate (testing the example)
multiplying and factoring skills (trying many examples)
Leading to More Problems
An almost-counter-example:
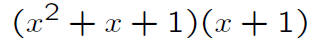
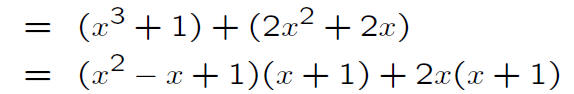
How to Answer a Question of Whether
Something Exists
Example 1. Is there a rational number r such that
r^2 = 1? Yes, there are two such numbers,
namely 1 and −1 since 1^2 = (−1)^2 = 1.
Example 2. Is there a rational number t such that
t^2 = 2? No. Suppose there were such a
t. Then t would be a rational zero of x^2 − 2 so by the Rational Zeros Theorem
the only
possibilities for t are ±1, ±2. But none of these is a zero of x^2 − 2 so no
such t exists.
Problem 2
Are there rational numbers a and b such that both a+ b and ab are integers but a and b are not?
The assignment is to attempt to solve the problem and to write about your attempt.
Typical Student Response to Problem 2
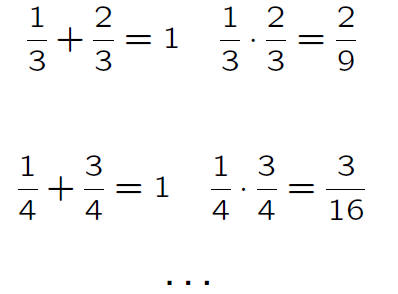
After examining many examples, I conclude there are no such numbers.
Instructor Response
Have you tried any improper fractions?
Negative numbers?
Student Response
Greater variety of examples
‘The product of two [nonintegral] fractions is a [nonintegral] fraction’ or ‘if the product of two fractions is an integer they must be reciprocals’.
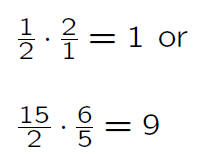
A greater number of students with a greater variety of
examples and nascent arguments
‘The sum of two [reduced] fractions is an integer only if they have the same
denominator.’
No complete (correct) arguments; no arguments using polynomials
Conclusions
1. Problem-solving occurs at a level lower than that of the course.
2. Students show increased motivation and surprising creativity.
3. Students have great difficulty reading mathematical statements.
4. Refining the problem statement can be part of the dialog.
5. More students show some progress, and some students show more progress at each feedback loop.
Corollaries: Principles for Designing
Assignments
1. Problems should be amenable to elementary approaches . . .
2. . . . but the instructor need not know the elementary solutions.
3. The problem statements should not be too complicated . . .
4. but the problems need not be stated with complete precision at the outset.
5. Assignments should have multiple feedback cycles.
Possible Extensions
Combine with in-class problem-solving and/or other types of writing assignments
Enrich prior (current, subsequent) courses in curriculum
to enhance conceptual repertoire for problem-solving
Reduced Fractions have the Same
Denominator If their Sum Is an Integer
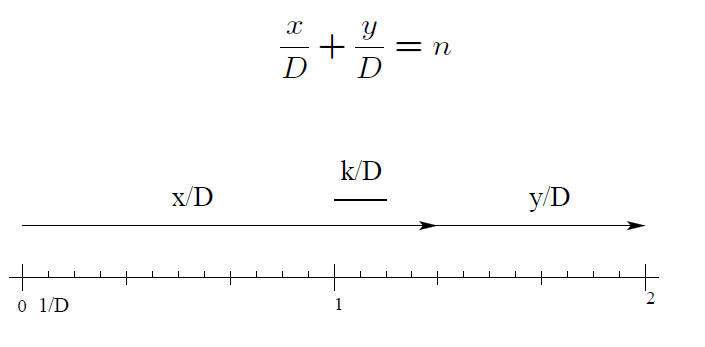
Proofs of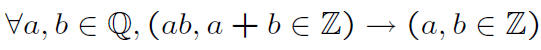 
Proof 1. By the Rational Zeroes Theorem,
every rational root of (x−a)(x−b) = x^2−(a+b)x+ab is an integer.
Proof 2. By the lemma,
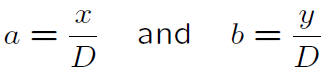(reduced).
So
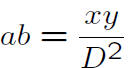
vas a reduced fraction, hence D = 1.