161 Practice Exam 2

Let

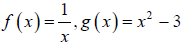
1. The domain of f is ______ and the domain of g is _____

2. Which function is even, and which function is odd. Prove your answer.

3. What is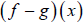? Is it even or odd?

4. What is 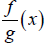and what is its domain?

5. Fi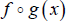nd and

6. Draw a picture of an even function on the left and an odd function on the right.

7. Fill in the blank: a function is one to one if ______________________

8. Give an example of a function that is one to one, and a function that is not one to one.

9. Draw a one to one function on the left and a function that is not one to one on the right.

Let the function F be defined by the ordered pairs:
{(0,1) , (1,2) , (2,4) , (3,8) , (4,16) , (5,32) , (6,64)}

10. What is the domain of F?

11. What is the range of F?

12. Is F a one to one function?

13. Describe as a set of ordered pairs.
Let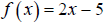

14. Prove that f is one to one.

15. Find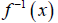
Let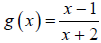

16. Prove that g is one to one.

17. Find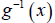

18. Find the vertex of the quadratic function 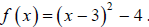The minimum value of f is ____ when x = ____

19. Find the vertex and the zeros of the quadratic function pictured below.

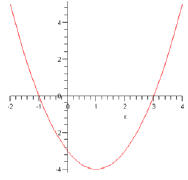
20. Over what intervals is the function positive, and over what interval is it negative?

21. Find the vertex of the quadratic function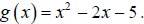 The minimum value of g is ____ when x = ____

22. Why is it clear that g has two real zeros?

23. Find them.

24. Solve for x: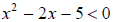

25. Solve for x: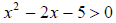

26. Find the two complex solutions to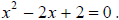 Make sure to write the answer in standard form.

27. Multiply: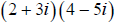

28. Divide: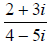

29. If you divide
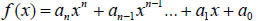by 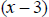and the remainder is 7, then ____

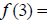30. Use synthetic division to divide:

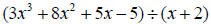
31. For ___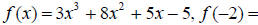

32. Use synthetic division to show that 3 is a zero of the polynomial

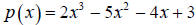
33. Use your answer above to factor p.

34. Find the other zeros of p and factor completely.