Topics in Mathematics
Algebra Curriculum
Focus
History of Algebra and Algebra Education
Definition of Algebra
NCTM Principles and Standards
Nebraska Algebra Standards
Typical United States Algebra Curriculum
Discussion
History of Algebra and Algebra Education
Algebra has been studied for many centuries. It can be traced back to the
Babylonians,
ancient Chinese, and Egyptians. Algebra was in what is referred to as the
“rhetorical”
stage. Problems were solved by the use of words and prose.
During the 3rd century, Diophantus of Alexandria (ca. 250) wrote the book
Arithmetica.
All but six of the original thirteen parts have been lost. The surviving parts
show that,
Diophantus interjected the use of symbols to represent unknowns into his work.
This
ushered algebra into the syncopated stage. In Arithmetica, however, Diophantus
solved
several practical problems and avoided any general procedures.
During the 5th and 6th centuries, many Indian and Arabic mathematicians became
very
prominent. The first being Aryabhatta (ca. 475 – ca. 550), whose book of the
same name,
Aryabhatta, dealt with work on linear and quadratic equations, and whose book
Brahmagupta presented the general solution to quadratic equations.
Al-Khwarizmi (ca. 825) was a 9th century Arabic mathematician that composed the
book
al-Kitab al-muhtasur fi hasib al-jabr wa’l-muqabala (“Compendium on calculation
by
completion and balancing” or “Science of cancellation and transposition”). If
you
translate the translation of the title, you loosely get “Science of equations”.
The book
produced a systematic consideration of algebra separate from number theory. It
also
provided general solutions to several different types of quadratic equations.
The Arabic
word “al-jabr”, that means completion, is the origins of the modern word
“algebra”.
The 12th century witnessed the Persian mathematician, Omar Khayyam (ca. 1044 –
ca.
1123), write a treatise on algebra. He followed Euclid’s (ca. 300 B.C.)
axiomatic methods
in its development and made the distinction between arithmetic and algebra. Also
during
the 12th century Al-Khwarizmi’s book was translated and made available to
western
mathematicians.
During the next century, Leonardo Fibonacci provided many important
contributions to
algebra. Fibonacci paved the way for others such as Luca Pacioli (1445-1517),
Robert
Recorde (1510-1558), Scipione del Ferro (c. 1465-1526), and Ludovico Ferrari
(1522-
1565).
Francois Viète (1540-1603) is credited with introducing the symbols that are
used in
algebra. Algebra entered its last stage of development at this time; the
symbolic stage.
Carl Friedrich Gauss (1777-1855) proved the Fundamental Theorem of Algebra in
his
doctoral thesis. The Fundamental Theorem of Algebra was first proposed by Girard
(1593 - 1632) in 1629.
Fundamental Theorem of Algebra: Given a polynomial equation of degree n, there
exists exactly n solutions to the equation.
Modern day proofs of the theorem rely on complex analysis and the inclusion of
complex
roots. The idea of complex roots was introduced sometime around the time of René
Descartes (1596 - 1650). It took some time for it to be fully accepted.
René Descartes is considered the “Father of Analytical Geometry” and is honored
with
the rectangular coordinate system being named after him (the “Cartesian Plane”).
Geometric concepts are now described by equations and symbolic expressions.
The 19th and 20th centuries have seen algebra become much more abstract. Algebra
no
longer includes only the theory of equations. It also involves game theory and
matrices. It
is used as a common thread in calculus, discrete mathematics, probability and
statistics,
and most other fields of mathematics, as well as in any discipline that has a
quantitative
aspect to it. Algebra has been described as the language of science.
The National Council of Teachers of Mathematics (NCTM) describes algebra as
being
“dynamic and a necessary vehicle for describing a changing world”.
Algebra education in my opinion has experienced two major influences. The first
being
the School Mathematics Study Group project that resulted from panic in the
United States
after the Russian launching of Sputnik. Prior to that, algebra instruction was
based on the
prior work of the mathematicians previously mentioned. For example, in the early
1940s
Clemson University was using a college algebra textbook written by Rosenbach and
Whitman. In the front of the book, honor is paid to Robert Recorde (1510-1558)
for his
influence on algebra. The book covers twenty topics and from a strictly symbolic
point of
view. The topics are:
I. Fundamental Operations
II. Factoring and Fractions
III. Exponents and Radicals
IV. Functions and Their Graphs
V. Equations and Their Solutions
VI. Systems of Linear Equations
VII. Quadratic Equations
VIII. System of Equations Involving Quadratics
IX. Ratio, Proportion, and Variation
X. Progressions
XI. Mathematical Induction and Binomial Theorem
XII. Inequalities
XIII. Complex Numbers
XIV. Theory of Equations
XV. Logarithms
XVI. Interest and Annuities
XVII. Permutations, Combinations, and Probability
XVIII. Determinants
XIX. Partial Fractions
XX. Infinite Series
Granted this is a college text, therefore some of the topics listed were not
covered in a
high school class and others were only briefly touched on in high school. The
point is that
these are the topics that the greats wrestled with and wrote about. The methods
used in
the text were more like a recipe than anything else.
Laws of signs
1. To add two numbers of like signs, add their absolute values and prefix
their common sign to the result.
2. To add two numbers of unlike signs, subtract the smaller absolute value
from the larger and …
No explanation provided!
After Sputnik was launched, the U.S. worried that the Russians were academically
ahead
of us. To fight this, the School Mathematics Study Group (SMSG) was created
under the
leadership of Edward Begle (1914 - 1978) of Yale University. A group of
university
mathematics professors decided what topics should be covered in the kindergarten
to
twelfth grade mathematics curriculum. The purpose of the curriculum was to
prepare
students to go on to college and study mathematics, science, and engineering.
The SMSG had its successes and its FAILURES. The main affects on high school
algebra, the introduction of set theory, and field theory. Another very
important overreaching
result was the publishing of the Mary Dolciani textbook series. This series
included Algebra: Structure and Method, probably the most popular and most used
high
school algebra book. As the text ran through several editions, concepts such as
matrices
and analytic geometry were introduced.
In the late 1980s and again in 2000, NCTM published sets of high school
mathematics
standards. The early set is responsible for the standards-based education reform
movement. NCTM went about its task different than SMSG did, by including K-12
teachers, business representatives, community college instructors, university
professors
and others in its discussions and deliberations. The result was a set of
standards that was
applicable to and “reachable” by all students.
The NCTM identified the fundamental components of algebraic thinking as:
• Understanding patterns, relations, and functions
• Representing and analyzing mathematical situations and structures using
algebraic symbols
• Using mathematical models to represent and understand quantitative
relationships
• Analyzing change in various contexts
These concepts are inherent in most modern day middle/high school algebra
textbooks.
Pedagogy based on Bruner’s and Piaget’s work is also present in most textbooks.
The
NCTM encourages the use of manipulatives to build a solid base for mathematical
learning. Students must pass through all of Bruner’s three stages. Therefore,
algebra
concepts are being presented earlier in the K-12 curriculum and the use of
manipulatives
is occurring at all levels.
The movement to base curriculum, instruction, and assessment on clearly defined
standards forces one to rethink the way in which algebra is learned as well as
taught.
Standards have placed the main emphasis on learning. We must emphasize the
issues this
causes and think about “thinking mathematically”.
Algebra education (as well as any mathematics education) cannot be broken down
into a
sequence of steps. Teacher development in algebra cannot be dominated by the
“how-to”
mentality. Algebra education and teacher development must prompt deep and
personal
reflection about learning. Learning algebra is constructive. Abstract concepts
must be
grounded in previously learned less abstract concepts.
Definition of Algebra
Reviewing the history of algebra gives clues to the meaning of “algebra”. A
common
perception is that algebra is the generalization of arithmetic. That is to say
that 2+3 =3+2
is generalized as x+ y = y + x. The former is true for one static example, while
the latter
is true for a more “general” dynamic situation. The letters are symbols used to
represent a
set of values, rather than a constant.
Algebra is in the symbolic stage of its development. The symbolism used not only
covers
representation of unknowns, but also covers operations and relations. The use of
this
symbolism constitutes a language.
A perusal of history highlights the importance that equations and their
solutions play in
algebra. The fundamental theorem indicates the importance of the role
polynomials and
polynomial equations play in algebra. The names of the books written as well as
the
authors tell us the importance of problem solving and equations.
Matrices and game theory, as well as other areas, are included in the study of
algebra.
Algebra is no longer seen as a collection of rules and methods of doing
mathematics.
Algebra is a process. Algebra is a systematic development. Your college studies
in
algebra show that algebra is an axiomatic system just like geometry. Mentioning
geometry, analytic geometry is a major part of algebra. Analytic geometry is the
marriage
of algebra and geometry.
So what is the definition of algebra?
NCTM Principles and Standards
The NCTM recommends that all five content strands be distributed over all grade
levels.
But, as the illustration below shows, they are not evenly distributed. Algebra
makes up
most of the recommended curriculum in grades 9-12. Algebra and geometry are the
bulk
of the curriculum in grades 6-8. In the Principles and Standards, the NCTM
proposes
proportionality as an integrative theme in the middle-grades mathematics
program.
Facility with proportionality develops through work in many areas of the
curriculum,
including ratio and proportion, percent, similarity, scaling, linear equations,
slope,
relative-frequency histograms, and probability. The understanding of
proportionality
should also emerge through problem solving and reasoning, and it is important in
connecting mathematical topics and in connecting mathematics and other domains
such
as science and art.
Distribution of Content Standards by Grade Band
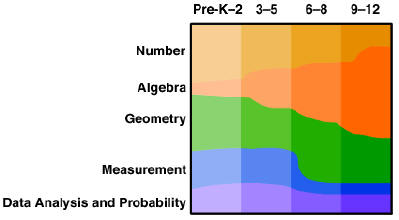
The NCTM recommendations for middle-grades mathematics have students learning
significant amounts of algebra and geometry throughout grades 6, 7, and 8.
Moreover,
students will see algebra and geometry as interconnected with each other and
with other
content areas in the curriculum. They will have experience with both the
geometric
representation of algebraic ideas, such as visual models of algebraic
identities, and the
algebraic representation of geometric ideas, such as equations for lines
represented on
coordinate grids. They will see the value of interpreting both algebraically and
geometrically such important mathematical ideas as the slope of a line and the
Pythagorean relationship. They also will relate algebraic and geometric ideas to
other
topics—for example, when they reason about percents using visual models or
equations
or when they represent an approximate line of fit for a scatter-plot both
geometrically and
algebraically. Students can gain a deeper understanding of proportionality if it
develops
along with foundational algebraic ideas such as linear relationships and
geometric ideas
such as similarity.
Students' understanding of foundational algebraic and geometric ideas should be
developed through extended experience over all three years in the middle grades
and
across a broad range of mathematics content, including statistics, number, and
measurement. How these ideas are packaged into courses and what names are given
to
the resulting arrangement are far less important than ensuring that students
have
opportunities to see and understand the connections among related ideas. This
approach
is a challenging alternative to the practice of offering a select group of
middle-grades
students a one-year course that focuses narrowly on algebra or geometry. All
middlegrades
students will benefit from a rich and integrated treatment of mathematics
content.
Instruction that segregates the content of algebra or geometry from that of
other areas is
educationally unwise and mathematically counterproductive.
As students move into high school the importance of algebra is to be amplified.
But as in
middle school, the NCTM recommends that it not be taught in isolation from other
areas
of mathematics and other disciplines. It recommends that a high school student’s
algebraic training prepare him/her for the “new calculus” taught in colleges and
universities.
ALGEBRA STANDARDS
Instructional programs from pre-kindergarten through grade 12
should enable all students to—
Understand patterns, relations, and functions
Pre-K–2 Expectations:
In pre-kindergarten through grade 2 all students should–
• sort, classify, and order objects by size, number, and other properties;
• recognize, describe, and extend patterns such as sequences of sounds and
shapes or
simple numeric patterns and translate from one representation to another;
• analyze how both repeating and growing patterns are generated.
Grades 3–5 Expectations:
In grades 3–5 all students should–
• describe, extend, and make generalizations about geometric and numeric
patterns;
• represent and analyze patterns and functions, using words, tables, and graphs.
Grades 6–8 Expectations:
In grades 6–8 all students should–
• represent, analyze, and generalize a variety of patterns with tables, graphs,
words,
and, when possible, symbolic rules;
• relate and compare different forms of representation for a relationship;
• identify functions as linear or nonlinear and contrast their properties from
tables,
graphs, or equations.
The study of patterns and relationships in the middle grades should focus on
patterns that
relate to linear functions, which arise when there is a constant rate of change.
Students
should solve problems in which they use tables, graphs, words, and symbolic
expressions
to represent and examine functions and patterns of change.
Grades 9–12 Expectations:
In grades 9–12 all students should–
• generalize patterns using explicitly defined and recursively defined
functions;
• understand relations and functions and select, convert flexibly among, and use
various representations for them;
• analyze functions of one variable by investigating rates of change,
intercepts, zeros,
asymptotes, and local and global behavior;
• understand and perform transformations such as arithmetically combining,
composing, and inverting commonly used functions, using technology to perform
such operations on more-complicated symbolic expressions;
• understand and compare the properties of classes of functions, including
exponential,
polynomial, rational, logarithmic, and periodic functions;
• interpret representations of functions of two variables .
High school students' algebra experience should enable them to create and use
tabular,
symbolic, graphical, and verbal representations and to analyze and understand
patterns,
relations, and functions with more sophistication than in the middle grades. In
helping
high school students learn about the characteristics of particular classes of
functions,
teachers may find it helpful to compare and contrast situations that are modeled
by
functions from various classes.
Represent and analyze mathematical situations and structures using algebraic
symbols
Pre-K–2 Expectations:
In prekindergarten through grade 2 all students should–
• illustrate general principles and properties of operations, such as
commutativity,
using specific numbers;
• use concrete, pictorial, and verbal representations to develop an
understanding of
invented and conventional symbolic notations.
Grades 3–5 Expectations:
In grades 3–5 all students should–
• identify such properties as commutativity, associativity, and distributivity
and use
them to compute with whole numbers;
• represent the idea of a variable as an unknown quantity using a letter or a
symbol;
• express mathematical relationships using equations.
Grades 6–8 Expectations:
In grades 6–8 all students should–
• develop an initial conceptual understanding of different uses of variables;
• explore relationships between symbolic expressions and graphs of lines, paying
particular attention to the meaning of intercept and slope;
• use symbolic algebra to represent situations and to solve problems, especially
those
that involve linear relationships;
• recognize and generate equivalent forms for simple algebraic expressions and
solve
linear equations
Working with variables and equations is an important part of the middle-grades
curriculum. Students' understanding of variable should go far beyond simply
recognizing
that letters can be used to stand for unknown numbers in equations.
Grades 9–12 Expectations:
In grades 9–12 all students should–
• understand the meaning of equivalent forms of expressions, equations,
inequalities,
and relations;
• write equivalent forms of equations, inequalities, and systems of equations
and solve
them with fluency—mentally or with paper and pencil in simple cases and using
technology in all cases;
• use symbolic algebra to represent and explain mathematical relationships;
• use a variety of symbolic representations, including recursive and parametric
equations, for functions and relations;
• judge the meaning, utility, and reasonableness of the results of symbol
manipulations, including those carried out by technology.
Fluency with algebraic symbolism helps students represent and solve problems in
many
areas of the curriculum. For example, proving that the square of any odd integer
is 1 more
than a multiple of 8 can involve representing odd numbers and operating on that
representation algebraically. Likewise, the equations in the figure below
suggest an
algebraic justification of a visual argument for the Pythagorean theorem. And
many
geometric conjectures—for example, the medians of a triangle intersect at a
point—can
be proved by representing the situation using coordinates and manipulating the
resulting
symbolic forms. Straightforward algebraic arguments can be used to show how the
mean
and standard deviation of a data set change if sample measurements are converted
from
square meters to square feet.
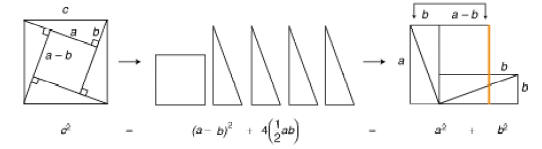
An algebraic explanation of a visual proof of the Pythagorean theorem
Students should be able to operate fluently on algebraic expressions, combining
them and
re-expressing them in alternative forms. These skills underlie the ability to
find exact
solutions for equations, a goal that has always been at the heart of the algebra
curriculum.
Even solving equations such as
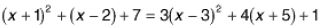
requires some degree of fluency. Finding and understanding the meaning of the
solution
of an equation such as
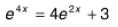
calls for seeing that the equation can be written as a quadratic equation by
making the
substitution u = e2x. (Such an equation deserves careful attention because one
of the roots
of the quadratic is negative.) Whether they solve equations mentally, by hand,
or using
CAS, students should develop an ease with symbols that enables them to represent
situations symbolically, to select appropriate methods of solution, and to judge
whether
the results are plausible.
Being able to operate with algebraic symbols is also important because the
ability to
rewrite algebraic expressions enables students to re-express functions in ways
that reveal
different types of information about them. For example, given the quadratic
function
f(x) = x2 – 2x – 3, some of whose graphical properties were discussed earlier,
students
should be able to reexpress it as f(x) = (x – 1)2 – 4, a form from which they
can easily
identify the vertex of the parabola. And they should also be able to express the
function
in the form f(x) = (x – 3)(x + 1) and thus identify its roots as x = 3 and x =
–1.
Use mathematical models to represent and understand quantitative relationships
Pre-K–2 Expectations:
In prekindergarten through grade 2 all students should–
• model situations that involve the addition and subtraction of whole numbers,
using
objects, pictures, and symbols.
Grades 3–5 Expectations:
In grades 3–5 all students should–
• model problem situations with objects and use representations such as graphs,
tables,
and equations to draw conclusions.
Grades 6–8 Expectations:
In grades 6–8 all students should–
• model and solve contextualized problems using various representations, such as
graphs, tables, and equations.
Grades 9–12 Expectations:
In grades 9–12 all students should–
• identify essential quantitative relationships in a situation and determine the
class or
classes of functions that might model the relationships;
• use symbolic expressions, including iterative and recursive forms, to
represent
relationships arising from various contexts;
• draw reasonable conclusions about a situation being modeled.
Analyze change in various contexts
Pre-K–2 Expectations:
In prekindergarten through grade 2 all students should–
• describe qualitative change, such as a student's growing taller;
• describe quantitative change, such as a student's growing two inches in one
year.
Grades 3–5 Expectations:
In grades 3–5 all students should–
• investigate how a change in one variable relates to a change in a second
variable;
• identify and describe situations with constant or varying rates of change and
compare
them.
Grades 6–8 Expectations:
In grades 6–8 all students should–
• use graphs to analyze the nature of changes in quantities in linear
relationships.
Grades 9–12 Expectations:
In grades 9–12 all students should–
• approximate and interpret rates of change from graphical and numerical data.
Nebraska Algebra Standards
The NEBRASKA DEPARTMENT OF EDUCATION ADMINISTRATIVE RULES
(TITLE 92, NEBRASKA ADMINISTRATIVE CODE) AS OF MAY 2005 provides the
curriculum requirements for the state K-12 schools in Rule 10, Section 4.
004 Curriculum and Standards
004.01 K-12 Curriculum. Quality Indicator: The curriculum is comprehensive,
coordinated, and sequential and is directed toward locally approved goals and
standards for student learning. The instructional program focuses on
achievement and provides for the needs of all students including learners with
disabilities and high ability learners. It draws upon research, best practice,
and
reputable theory.
004.01B By July 1, 2003, each school district either adopts measurable quality
academic content standards for reading, writing, mathematics, science, and
social
studies/history that are the same as those found in Appendices A through D of
this
Chapter or adopts local content standards approved by the Commissioner as equal
to
or exceeding in rigor the standards in Appendices A through D of this Chapter.
By
July 1, 2003, nonpublic schools have local academic content standards for
reading,
writing, mathematics, science, and social studies/history approved by the local
governing body.
004.01C Districts electing not to adopt the state academic content standards
submit
the local academic content standards to the Commissioner for approval as equal
to or
exceeding in rigor the state standards according to at least one of the
following
criteria.
• 004.01C1 The local standards contain the same content organized in a different
way.
• 004.01C2 The local standards include more components of a content area. An
example would be mathematic standards that include vectors, which is a
component of algebra, which is not covered in Appendices A through D of this
Chapter.
• 004.01C3 The local standards cover more content areas in a subject. An example
would be mathematic standards that include the content area of fractals, which
is
the study of repeated patterns, which is not covered in Appendices A through D
of this Chapter.
Middle School Curriculum
004.03A3 Mathematics. The curriculum includes practice in numeration,
computation, estimation, problem solving, geometry/spatial concepts, and
measurement. It introduces algebraic and statistical concepts and provides
opportunities for students to develop understanding of the structure of
mathematics.
High School Curriculum
004.04B3 Mathematics - 40 instructional units. The curriculum includes
communicating, reasoning, problem solving, numeration, computation, estimation,
measurement, geometry, data analysis, probability and statistical concepts, and
algebraic concepts.
The state of Nebraska has based its mathematics standards on those of the NCTM.
The
Nebraska Mathematics Standards (NMS) includes four benchmark years (e.g. end of
first
grade, end of fourth grade, end of eighth grade and end of twelfth grade). The
NMS are
broken into process standards and content standards. The process standards are
divided
into the following:
• Problem Solving
• Mathematical Communication
• Mathematical Reasoning
• Mathematical Connections
• Mathematical Representation
The content standards are divided into the following strands:
• Numeration/Number Sense
• Computation/Estimation
• Measurement
• Geometry/Spatial Concepts
• Data Analysis, Probability, and Statistical Concepts
• Algebraic Concepts
The Algebraic Concepts category contains three or four standards per benchmark
grade.
Refer to the copy of the NMS provided.
Typical United States Algebra Curriculum
K-12 Algebra instruction in the U.S. tends to follow a standardized curriculum.
The
curriculum for the most part follows that described by Dolciani in her popular
textbooks.
Dolciani is no longer publishing. Ron Larson from Penn State University at Erie,
is the
lead author for Houghton Mifflin’s most popular algebra series. This series
replaced
Dolcini’s.
A quick perusal of the Algebra 1 book shows the content divided into
1. Connections to Algebra
2. Properties of Real Numbers
3. Solving Linear Equations
4. Graphing Linear Equations and Functions
5. Writing Linear Equations
6. Solving and Graphing Linear Inequalities
7. Systems of Linear equations and Inequalities
8. Exponents and Exponential Functions
9. Quadratic Equations and Functions
10. Polynomials and Factoring
11. Rational Equations and Functions
12. Radicals and Connections to Geometry
A quick perusal of the Algebra 2 book shows the content divided into
1. Equations and Inequalities
2. Linear Equations and Functions
3. Systems of Linear Equations and Inequalities
4. Matrices and Determinants
5. Quadratic Functions
6. Polynomials and Polynomial Functions
7. Powers, Roots, and Radicals
8. Exponential and Logarithmic Functions
9. Rational Equations and Functions
10. Quadratic Relations and Conic Sections
11. Sequences and Series
12. Probability and Statistics
13. Trigonometric Ratios and Functions
14. Trigonometric Graphs, Identities, and Equations
Skimming a typical section such as Section 6.2 of Algebra 1, shows that the book
is still
very exercise based. There are problems (tasks), but the majority of the text is
comprised
of exercises and an emphasis on symbolic manipulation.
Refer to the sample unit provided.
In recent years integrated mathematics curriculums have been emerging. A very
good
example is the Core-Plus Mathematics Project (published as Contemporary
Mathematics
in Context). Scanning through the contents of Course 1 (Freshman Mathematics)
you see
seven units:
1. Patterns in Data
2. Linear Models
3. Patterns of Change
4. Graph Models
5. Patterns in Space and Visualization
6. Simulation Models
7. Exponential Models
Each unit consists of four to five lessons. The lessons are centered about
meaningful,
applicable investigations that are problematic. Problematic means that the
investigations
promote learning by building on previous knowledge and avoid repetitious
exercises that
concentrate on isolated concepts.
The course integrates algebra and functions, statistics and probability,
geometry and
trigonometry, and discrete mathematics. Each investigation involves more than
one of
these categories at a time. Algebra of course is a common thread throughout all
lessons.
Refer to the sample unit provided.


