Try the Free Math Solver or Scroll down to Tutorials!

Enter expression, e.g. (x^2-y^2)/(x-y)

Enter expression, e.g. x^2+5x+6

Enter expression, e.g. (x+1)^3

Enter a set of expressions, e.g. ab^2,a^2b

Enter equation to solve, e.g. 2x+3=4

Enter equation to graph, e.g. y=3x^2-1

Depdendent Variable

Number of equations to solve:

Equ. #1:

Equ. #2:

Equ. #3:

Equ. #4:

Equ. #5:

Equ. #6:

Equ. #7:

Equ. #8:

Equ. #9:

Solve for:

Enter inequality to solve, e.g. 2x+3>4

Enter inequality to graph, e.g. y<3x^2-1

Dependent Variable

Number of inequalities to solve:

Ineq. #1:

Ineq. #2:

Ineq. #3:

Ineq. #4:

Ineq. #5:

Ineq. #6:

Ineq. #7:

Ineq. #8:

Ineq. #9:

Solve for:

Math solver on your site

Please use this form if you would like
to have this math solver on your website,
free of charge.

Name:

Email:

Your Website:

Msg:

Factoring Polynomials

Finding GCF (Greatest Common Factor)

•the largest natural number that divides all given numbers evenly

Find the GCF of 24 and 60

List Factors	Prime Factorization
Factors of 24: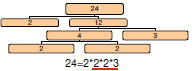
1 2 3 4 6 8 12 24
Factors of 60: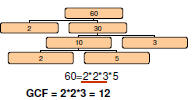
1 2 3 4 5 6 10 12 15 20 30 60

Finding GCF Of Variables

Find the GCF of x²y³z and x³z

Consider each variable that exists in each Monomial

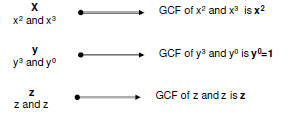
Therefore, GCF of x²y³z and x³z is x²*1*z = x²z

The simplest method of factoring a polynomial is to factor out
the greatest common factor (GCF) of each term.

Example: Factor 18x³ + 60x.

GCF of 18 and 60 = 6	Determine GCF of the coefficients of each term.
GCF x³ and x = x	Determine GCF of the variables in each term.
GCF = 6x	The GCF of the polynomial is the product of the GCF’s found above
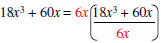	Factored form GCF ->*
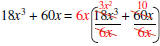	Rewrite and Simplify within the
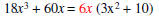	parentheses.
Check the answer by multiplication.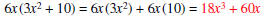

The simplest method of factoring a polynomial is to factor out
the greatest common factor (GCF) of each term.

Example: Factor 24x²y + 60x³

GCF of 24 and 60 = 12	Determine GCF of the coefficients of each term.
GCF x²y and x³ = x²	Determine GCF of the variables in each term.
GCF = 12x²	The GCF of the polynomial is the product of the GCF’s found above.
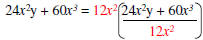	Factored form GCF -> *
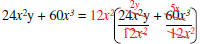	Rewrite and Simplify within the parentheses.

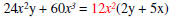Check the answer by multiplication.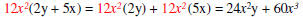

The simplest method of factoring a polynomial is to factor out
the greatest common factor (GCF) of each term.

Example: Factor 4x² -12x+ 20.

GCF of 4, 12 and 20 = 4	Determine GCF of the coefficients of each term.
GCF x², x , 0 = N/A	Determine GCF of the variables in each term.
GCF = 4	The GCF of the polynomial is the product of the GCF’s found above.
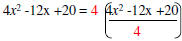	Factored form GCF ->*
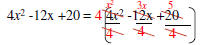	Simplify.

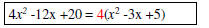Check the answer by multiplication.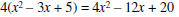

A common binomial factor can be factored out of certain
expressions.

Example: Factor the expression 5(x + 1) – y(x + 1).
5(x + 1) – y(x + 1) = (5 – y)(x + 1)
(5 – y)(x + 1) = 5(x + 1) – y(x + 1) Check.

Some polynomials can be factored by grouping terms to produce
a common binomial factor.

Examples: 1. Factor xy + 2y + 7x + 14.

xy + 2y + 7x + 14.	= (xy + 2y) + (7x + 14).	Group terms.
	= y(x + 2) + 7(x + 2)	Factor each pair of terms.
	= (x + 2)(y + 7)	Factor out the common binomial.

2. Factor 6x³ - 8x² + 3xy - 4y.

6x³ - 8x² + 3xy - 4y.	= (6x³ - 8x²)+ (3xy - 4y).	Group terms.
	= 2x²(3x – 4) + y(3x – 4)	Factor.
	= (2x² + y)(3x – 4)

Some polynomials can be factored by grouping terms to produce
a common binomial factor.

Examples: 3. Factor 2xy + 3y – 4x – 6.

2xy + 3y – 4x – 6	= (2xy + 3y) – (4x + 6)	Group terms.
	= (2x + 3)y – (2x + 3)2	Factor each pair of terms.
	= (2x + 3)(y – 2)	Factor out the common binomial.

4. Factor 2a² + 3bc – 2ab – 3ac.

2a² + 3bc – 2ab – 3ac	= 2a² – 2ab – 3ac + 3abc	Rearrange terms.
	= (2a² – 2ab) – (3ac + 3bc)	Group terms.
	= 2a(a – b) – 3c(a – b)	Factor.
	= 2a(a – b) – 3c(a – b)	Factor.
	= (2a – 3c)(a – b)

Your Math Help is on the Way!

More Math Help

Factoring Polynomials

Finding GCF (Greatest Common Factor)

Finding GCF Of Variables