The General, Linear Equation

2.1.2 The Wronskian

The Wronskian determinant of a pair of functions is defined as follows:

Definition 2.1.3

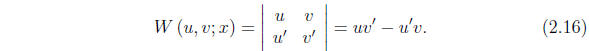
We often write W (u, v; x) = W (x) for short. When we do this we need to
remember that we have a specific pair of functions u and v in mind, and that
the sign of the Wronskian changes if we interchange them.

Theorem 2.1.6 Let u and v be solutions of equation (2.7). If is any
point of [a, b] and 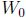the value of the Wronskian there, then, at any point x
of [a, b],

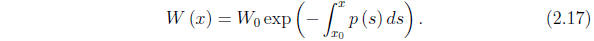
Proof: Differentiating W as defined in equation (2.16) gives W' = uv''−u''v.
Substituting for the second derivatives from the equation (2.7), satisfied by
each of u and v, then gives W' = −pW. The conclusion follows from this.

An immediate deduction from this is the following:

Corollary 2.1.1 The Wronskian of a pair of solutions of a linear, homogeneous
equation (2.3) either vanishes identically on the entire interval [a, b]
or does not vanish at any point of the interval.

The Wronskian is precisely the determinant appearing in the systems
(2.13) and (2.14) above. When the Wronskian vanishes, the solutions and
are linearly dependent, and when the Wronskian does not vanish they
are linearly independent and therefore constitute a basis. This proves the
following:

Theorem 2.1.7 A necessary and sufficient condition for a pair 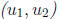of
solutions of equation (2.7) to be a basis for that equation is that its Wronskian
W 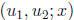not vanish on [a, b].

Remark: If a pair of solutions and is chosen “at random,” i.e., if
their initial data are assigned randomly, we would expect that W ≠ 0; in
this sense it would take a “peculiar” choice of solutions for that pair to be
linearly dependent.

The expression (2.17) for the Wronskian may be used to find a formula
for a second solution v of equation (2.7) if we know one solution u. Suppose
one such solution u (not identically zero) is known on [a, b]. Pick a point
where u ≠ 0 and define

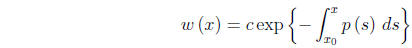
where c is not zero but is otherwise arbitrary. Write

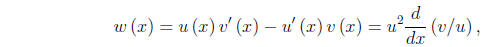
so that

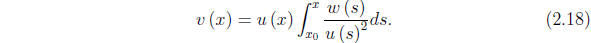
This formula defines v on an interval containing on which u does not vanish.
It is straightforward to check that v is indeed a solution of equation (2.7)
on such an interval, and that the pair u, v has the nonvanishing Wronskian
w there.

PROBLEM SET 2.1.1

1. Verify equation (2.2) in detail for the special case when n = 2 and the
operator L is defined by equation (2.5). Using equation (2.2), verify Lemma
2.0.2.

2. Let L be the second-order operator defined by equation (2.5). Suppose k
functions 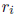(x) , i = 1, . . . , k are given on the interval [a, b] and the corresponding
k initial-value problems



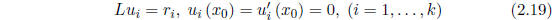
are solved for the k functions , i = 1, . . . , k. Define .
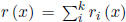Show that the unique solution of the initial value problem Lu = r, u () =
u' () = 0 is

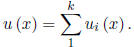
3. In equation (2.7) let the interval be [-1, 1]. Can continuous coefficients q
and p be chosen such that u (x) = x² is a solution of this equation?

4. Let u (x) = x³ on [-1, 1] and define v (x) = -x³ on [-1, 0] and v (x) = +x³
on (0, 1]. Verify that v is C² on [-1, 1]. Calculate W (u, v; x). Are these
functions linearly dependent on [-1, 1]?

5. The fundamental theorem of algebra states that a polynomial of degree n
can have no more than n distinct zeros. Draw the conclusion of Example
2.1.1 from this.

6. Show that the three functions sin(x), sin(2x), sin(3x) are linearly independent
on any nontrivial interval of the x axis.

7. For the equation u''+u = 0, cos x and sin x form a basis of solutions. Verify
that cos (x + a) and sin (x + a) are also solutions if a is any constant. Use
this and the uniqueness theorem to infer the trigonometric addition theorems

cos (x + a) = cos a cos x - sin a sin x,
sin (x + a) = cos a sin x + sin a cos x.

8. Find bases of solutions for the following equations:

a) u'' = 0;
b) u'' + 2u' = 0;
c) u'' + xu' = 0.

9. Consider the equation u'' + u = 0. Under what conditions on the constants
a, b, c, d is the pair



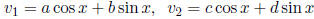
a basis of solutions for this equation?

10. Consider the equation u'' - u = 0. Under what conditions on the constants
a, b, c, d is the pair



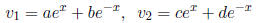
a basis of solutions for this equation?

11. Show that the functions 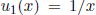and 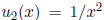form a basis of
solutions for the equation



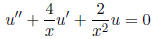
on any interval excluding the origin.

12. Same as the preceding problem for the functions = sin x − x cos x , =
cos x + x sin x and the differential equation

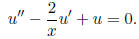
13. Verify that the second solution given in the formula (2.18) is linearly independent
of u on intervals on which u does not vanish.

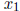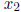14. Let u be a solution of (2.7) vanishing at the endpoints and of an
interval but not vanishing in between. Show that the formula (2.18), with
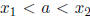, leads to finite limiting values for the second solution v at
and 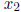, and find these limits.

15. A second-order equation

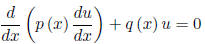
is said to be in ”self-adjoint” form. What condition on the function p is
needed for the existence theorem 2.1.1 to hold? Show that the Wronskian
of such a self-adjoint equation is, except for a multiplicative constant, p^-1.

16. For the equation

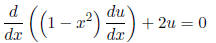
• On what interval does the existence theorem guarantee a solution?

• Verify that 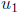= x is a solution.

• Find a second solution in an interval containing the origin. How far
can this interval extend on each side of the origin?

17. Let u and v be C² functions on an interval I, and suppose their Wronskian
uv' − u'v does not vanish on I. Show that their zeros separate each other,
i.e., between any two consecutive zeros of u there is exactly one zero of v
and vice versa.

18. Consider the equation u'' +p(x)u' +q(x)u = 0 where p and q are continuous
on the entire real axis R. Suppose further that q(x) < 0 there. Show that if
u is not identically zero, it can have at most one zero on R.

19. Let u and v be given C² functions on an interval [a, b] whose Wronskian
nowhere vanishes there. Show that there is a differential equation of the
form (2.7) for which u and v form a basis of solutions.

20. Consider the initial-value problem on the interval [−1, 1]

u'' + q (x) u = 0, u (−1) = 1, u' (−1) = 0,

where the coefficient q is the sectionally continuous function

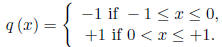
Find a function u satisfying the initial conditions, C¹ on the interval [−1, 1],
and satisfying the equation on the intervals [−1, 0) and (0, 1].

21. Suppose p and q are continuous functions on the symmetric interval [−a, a]
and satisfy the further conditions

p(−x) = −p(x) and q(−x) = q(x)

there; i.e., p is an odd function and q is even. For the differential equation
u'' + p(x)u' + q(x)u = 0 show

(a) If u(x) is a solution then so is v(x) = u(−x).

(b) There exists a basis of solutions 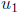, 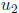of which one is even on the
interval, the other odd.