Examples of direct proof and disproof

This lecture does more examples of direct proof and disproof of quantified
statements, based on section 1.6 of Rosen (which you still don’t have to read yet).

1 Announcements

Proficiency exam results were emailed out to everyone yesterday afternoon
(or this morning in one case). If you took the exam and haven’t got your
results, contact Eric Shaffer. Today is the last day to change your registration
online.

2 Recap

Last class, we saw how to prove a universal (“for all”) claim and how to prove
an existential (“there exists”) claim. Proving the existential claim was easy:
we just showed our reader a specific example with the required properties.
For example:

Claim: There is an integer x such that x^2 = 1.
Proof: Consider 1. 1 is an integer and its square is 1.

Proofs for universal claims were more involved, because we needed to pick
a representative value x and to give a general argument that worked for any choice of x

When we grade proofs of universal claims, a common way to lose a lot of
points is to show that the claim holds for one specific example rather than
giving a general argument. This is a very serious flaw.

We also occasionally see students constructing a general argument when
they only needed a single specific counter-example. This is a less serious bug,
but it’s still a bug, because it makes your proof unnecessarily abstract and
harder to read.

3 Another example of direct proof involving odd and even

Last class, we proved that:

Claim 1 For every rational number q, 2q is rational.

We used a so-called “direct proof,” in which the proof proceeded in a more-
or-less straight line from the given facts to the desired conclusion, applying
some definitions of key concepts along the way.

Here’s another claim that can be proved in this straightforward manner.

Claim 2 For any integer k, if k is odd then k^2 is odd.

This has a slightly different form from the previous claim: 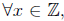if P(x), then Q(x)

Before doing the actual proof, we first need to be precise about what we
mean by “odd”. And, while we are on the topic, what we mean by “even.”

Definition 1 An integer n is even if there is an integer m such that n = 2m.

Definition 2 An integer n is odd if there is an integer m such that n = 2m + 1.

Such definitions are sometimes written using the jargon “has the form,” as
in “An integer n is even if it has the form 2m, where m is an integer.”

We’ll assume that it’s obvious (from our high school algebra) that every
integer is even or odd, and that no integer is both even and odd.

Using these definitions, we can prove our claim as follows:

Proof of Claim 2: Let k be any integer and suppose that k is odd.
We need to show that k^2 is odd.

Since k is odd, there is an integer j such that k = 2j + 1. Then
we have

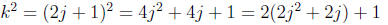
Since j is an integer, 2j^2 + 2j is also an integer. Let’s call it p.
Then k^2 = 2p + 1. So, by the definition of odd, k^2 is odd.

As in the proof last class, we used our key definition twice in the proof:
once at the start to expand a technical term (“odd”) into its meaning, then
again at the end to summarize our findings into the appropriate technical
terms.

Notice that we used a different variable name in the two uses of the
definition: j the first time and p the second time. It’s important to use a
fresh variable name each time you expand a definition like this. Otherwise,
you could end up forcing two variables (e.g. k and k^2) to be equal when that
isn’t (or might not be) true.

At the start of the proof, notice that we chose a random (or “arbitrary”
in math jargon) integer k, like last time. However, we also “supposed” that
the hypothesis of the if/then statement was true. It’s helpful to collect up
all your given information right at the start of the proof, so you know what
you have to work with.

The comment about what we need to show is not necessary to the proof.
It’s sometimes included because it’s helpful to the reader. You may also want
to include it because it’s helpful to you to remind you of where you need to
get to at the end of the proof.

Similarly, introducing the variable p isn’t really necessary with a claim
this simple. However, using new variables to create an exact match to a
definition may help you keep yourself organized.

4 Disproving a universal statement

Now, how about this claim?

Claim 3 For every rational number q, there is a rational number r such that qr = 1.

Or, in math jargon, every rational number has a (multiplicative) inverse.
This isn’t true, is it? Zero doesn’t have an inverse.

In general, a statement of the form “for all x in A, P(x)” is false exactly
when there is some value y in A for which P(y) is false. So, to disprove a
universal claim, we are proving an existential statement. So it’s enough to
exhibit one concrete value for which the claim fails. In this case, our disproof
is very simple:

Disproof of Claim 3: This statement isn’t true, because we know
from high school algebra that zero has no inverse.

5 Disproving an existential statement

There’s a general pattern here: the negation of 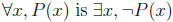. So the
negation of a universal claim is an existential claim. Similarly the negation of
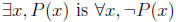. So the negation of an existential claim is a universal
one.

So, suppose we want to prove something like

Claim 4 There is an integer k such that k is odd and k^2 is even.
Disproving this claim is the same as proving

Claim 5 There is no integer k such that k is odd and k^2 is even.
Which is the same as

Claim 6 For every integer k, it is not the case that k is odd and k^2 is even.
At this point, it helps to use our logical equivalences to rephrase as

Claim 7 For every integer k, if k is odd then k^2 is not even.

If this last rephrasing isn’t obvious, let P(k) be “k is odd” and Q(k) be “k^2
is even”. Then this last step started with the claim 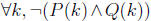. This
is equivalent to 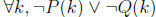by DeMorgan’s laws. This is equivalent
to 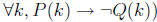, because 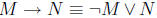. You probably wouldn’t
give all this detail in a proof, but you might need to work through it for
yourself on your scratch paper, to reassure yourself that your rephrasing was
legit.

Suppose that we are willing to believe that every integer is either even or
odd. It is possible to prove this from more basic properties of the integers,
but we’ll take it as obvious. Then we can rephrase our claim as:

Claim 8 For every integer k, if k is odd then k^2 is odd.
This is the universal claim that we proved at the start of the lecture.

6 Summary

So, our general pattern for selecting the proof type is:

Both types of proof start off by picking an element x from the domain
of the quantification. However, for the general arguments, x is a random
element whose identity you don’t know. For the proofs requiring specific
examples, you can pick x to be your favorite specific concrete value.

7 Another direct proof example

Here’s another direct proof example. First, let’s define

Definition 3 An integer n is a perfect square if n = k^2 for some integer k.

Consider the claim:

Claim 9 For any integers m and n, if m and n are perfect squares, then so is mn.

Proof: Let m and n be integers and suppose that m and n are
perfect squares.

By the definition of “perfect square”, we know that m = k^2 and
n = j^2, for some integers k and j. So then mn is k^2j^2, which is
equal to (kj)^2. Since k and j are integers, so is kj. Since mn
is the square of the integer kj, mn is a perfect square, which is
what we needed to show.

Notice that the phrase “which is what we needed to show” helps tell the
reader that we’re done with the proof. It’s polite to indicate the end in
one way or another. In typed notes, it may be clear from the indentation.
Sometimes, especially in handwritten proofs, we put a box or triangle of dots
or Q.E.D. at the end. Q.E.D. is short for Latin “Quod erat demonstrandum,”
which is just a translation of “what we needed to show.”

8 Vacuous truth

Consider the following claim:

Claim 10 For all natural numbers n, if 14 + n < 10, then n wood elves will
attack Siebel Center tomorrow.

I claim this is true, a fact which most students find counter-intuitive. In fact,
it wouldn’t be true if n was declared to be an integer.

Notice that this statement has the form 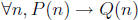. Let’s consider
some particular choice for n, e.g. n = i. Because i has to be a natural
number, i.e. no smaller than zero, P(i) is false. Therefore, our conventions
about the truth values for conditional statements imply that P(i) -> Q(i) is
true. This argument works for all natural numbers that we could substitute
for n. So 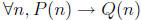is true.

Because even mathematicians find such statements a bit wierd, they typically
say that such a claim is vacuously true, to emphasize to the reader
that it is only true because of this strange convention about the meaning of
conditionals.