EASY PUTNAM PROBLEMS
Remark. The problems in the Putnam Competition are usually
very hard, but practically
every session contains at least one problem very easy to solve—it still may need
some sort
of ingenious idea, but the solution is very simple. This is a list of “easy”
problems that have
appeared in the Putnam Competition in past years—Miguel A. Lerma
2009-A1. Let f be a real-valued function on the plane such that for every
square ABCD in the
plane, f(A)+ f(B)+ f(C)+ f(D) = 0. Does it follow that f(P) = 0 for all points P
in the plane?
2009-B1. Show that every positive rational number can be written as a
quotient of products of
factorials of (not necessarily distinct) primes. For example,
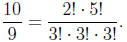
2008-A1. Let f : R2 → R be a function such that f(x, y) + f(y,
z) + f(z, x) = 0 for all
real numbers x, y, and z. Prove that there exists a function g : R → R such that
f(x, y) = g(x) − g(y) for all real numbers x and y.
2008-A2. Alan and Barbara play a game in which they take turns filling
entries of an initially
empty 2008 × 2008 array. Alan plays first. At each turn, a player chooses a real
number and places it in a vacant entry. The game ends when all the entries are
filled.
Alan wins if the determinant of the resulting matrix is nonzero; Barbara wins if
it is
zero. Which player has a winning strategy?
2008-B1. What is the maximum number of rational points that can lie on a
circle in R2 whose
center is not a rational point? (A rational point is a point both of whose
coordinates
are rational numbers.)
2007-A1. Find all values of α for which the curves
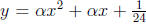and 
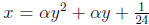
are tangent to each other.
2007-B1. Let f be a polynomial with positive integer coefficients. Prove
that if n is a positive
integer, then f(n) divides f(f(n) + 1) if and only if n = 1. [Note: one must
assume
f is nonconstant.]
2006-A1. Find the volume of the region of points (x, y, z) such that
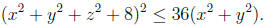
2006-B2. Prove that, for every set
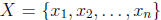of n real numbers, there exists a nonempty
subset S of X and an integer m such that
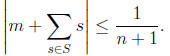
2005-A1. Show that every positive integer is a sum of one or more numbers
of the form 2r3s,
where r and s are nonnegative integers and no summand divides another. (For
example,
23 = 9 + 8 + 6.)
2005-B1. Find a nonzero polynomial P(x, y) such that
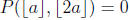for all real numbers a.
(Note: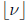 
is the greatest integer less than or
equal to v.)
2004-A1. Basketball star Shanille O’Keal’s team statistician keeps track
of the number, S(N),
of successful free throws she has made in her first N attempts of the season.
Early
in the season, S(N) was less than 80% of N, but by the end of the season, S(N)
was
more than 80% of N. Was there necessarily a moment in between when S(N) was
exactly 80% of N?
2004-B2. Let m and n be positive integers. Show that
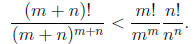
2003-A1. Let n be a fixed positive integer. How many ways are there to
write n as a sum of
positive integers,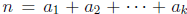 
, with k an arbitrary
positive integer and
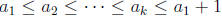? For example, with n = 4 there are four
ways: 4, 2+2,
1+1+2, 1+1+1+1.
2002-A1. Let k be a fixed positive integer. The n-th derivative of
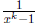has the form P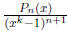
where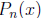 
is a polynomial. Find
.
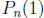2002-A2. Given any five points on a sphere, show that some four of them
must lie on a closed
hemisphere.
2001-A1. Consider a set S and a binary operation *, i.e., for each a, b ∈
S, a * b ∈ S. Assume
(a *b) * a = b for all a, b ∈ S. Prove that a * (b * a) = b for all a, b ∈ S.
2000-A2. Prove that there exist infinitely many integers n such that n,
n+1, n+2 are each the
sum of the squares of two integers. [Example: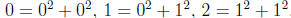 
.]
1999-A1. Find polynomials f(x), g(x), and h(x), if they exist, such that
for all x,
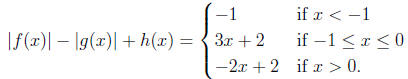
1998-A1. A right circular cone has base of radius 1
and height 3. A cube is inscribed in the
cone so that one face of the cube is contained in the base of the cone. What is
the
side-length of the cube?
1997-A5. Let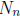 
denote the number of
ordered n-tuples of positive integers
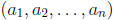such
that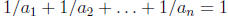 
. Determine whether
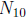is even or odd.
1988-B1. A composite (positive integer) is a product ab with a and b not
necessarily distinct
integers in {2, 3, 4, . . . }. Show that every composite is expressible as
xy+xz+yz+1,
with x, y, and z positive integers.