Try the Free Math Solver or Scroll down to Tutorials!

Enter expression, e.g. (x^2-y^2)/(x-y)

Enter expression, e.g. x^2+5x+6

Enter expression, e.g. (x+1)^3

Enter a set of expressions, e.g. ab^2,a^2b

Enter equation to solve, e.g. 2x+3=4

Enter equation to graph, e.g. y=3x^2-1

Depdendent Variable

Number of equations to solve:

Equ. #1:

Equ. #2:

Equ. #3:

Equ. #4:

Equ. #5:

Equ. #6:

Equ. #7:

Equ. #8:

Equ. #9:

Solve for:

Enter inequality to solve, e.g. 2x+3>4

Enter inequality to graph, e.g. y<3x^2-1

Dependent Variable

Number of inequalities to solve:

Ineq. #1:

Ineq. #2:

Ineq. #3:

Ineq. #4:

Ineq. #5:

Ineq. #6:

Ineq. #7:

Ineq. #8:

Ineq. #9:

Solve for:

Math solver on your site

Please use this form if you would like
to have this math solver on your website,
free of charge.

Name:

Email:

Your Website:

Msg:

Rational Number Ideas and Symbols

6.1 Rational Number Ideas and Symbols
	6.1.1. Rational Number Uses and Models
		6.1.1.1. Models for rational numbers
			6.1.1.1.1. Used to describe a quantity between 0 and 1
			6.1.1.1.2. identify the whole representing the numeral 1
			6.1.1.1.3. separate the whole into equal parts
			6.1.1.1.4. use an ordered pair of integers to describe the portion of the whole under consideration
		6.1.1.2. Identifying the whole and separating it into equal parts
			6.1.1.2.1. Egg carton fractions
				6.1.1.2.1.1.
				6.1.1.2.1.2.
			6.1.1.2.2. Integer Rods
				6.1.1.2.2.1.
				6.1.1.2.2.2.
			6.1.1.2.3. Make your own fraction kit
				6.1.1.2.3.1.
			6.1.1.2.4.
		6.1.1.3. Using two integers to describe part of a whole
			6.1.1.3.1. Need more language to describe part-whole relationship
			6.1.1.3.2. number of pieces of interest vs. number of pieces found in the original whole
	6.1.2. Defining Rational Numbers
		6.1.2.1. Definition of a rational number: A number is a rational number if and only if it can be represented by a pair of integers, a/b, where b ≠ 0 and a/b represents the quotient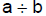
	6.1.3. Using Fractions to Represent Rational Numbers
		6.1.3.1. Fractions and Equivalent Fractions
			6.1.3.1.1. Definition of a fraction: A fraction is a symbol, a/b, where a and b are numbers and b ≠ 0. Here, a is the numerator of the fraction and b is the denominator of the fraction
			6.1.3.1.2. Proper fraction: when the numerator of the fraction is less than the denominator of the fraction and both the numerator and the denominator are integers
			6.1.3.1.3. Improper fraction: when the numerator of the fraction is greater than the denominator of the fraction (fractions with non-integers in the numerator or denominators are also improper)
			6.1.3.1.4. Definition of equivalent fractions : Two fractions, a/b and c/d, are equivalent fractions if and only if ad = bc
			6.1.3.1.5. Paper folding model
		6.1.3.2. Using fractions to represent rational numbers
			6.1.3.2.1. every rational number can be represented by an integer in the numerator and the denominator
			6.1.3.2.2. sometimes rational numbers are represented by non-integers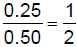 in a ratio
		6.1.3.3. The Fundamental Law of Fractions: Given a fraction a/b and a number c ≠ 0,
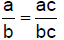		6.1.3.4. Fractions in simplest form
			6.1.3.4.1. Description of the simplest form of a fraction: a fraction representing a rational number is in simplest form when the numerator and the denominator are both integers that are relatively prime and the denominator is greater than zero.
				6.1.3.4.1.1. Finding equivalent fractions on the number line
				6.1.3.4.1.2. Folding paper
				6.1.3.4.1.3. Using a calculator
				6.1.3.4.1.4. Using Integer rods
	6.1.4. Using Decimals to Represent Rational Numbers
		6.1.4.1. Decimals
			6.1.4.1.1. Description of a decimal: A decimal is a symbol that uses a base-ten placevalue system with tenths and multiples of tenths to represent rational numbers
			6.1.4.1.2. decimal point divides the decimal portion of the number from the whole number portion of the number
			6.1.4.1.3. Using base ten blocks to explore decimals – see p. 287-8
		6.1.4.2. Expanded notation
			6.1.4.2.1.
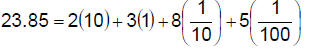		6.1.4.3. Writing a decimal for a fraction
			6.1.4.3.1. 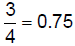- divide 3 by 4 to get the decimal equivalent
			6.1.4.3.2. 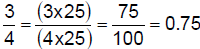- use the Fundamental Law of Fractions
			6.1.4.3.3. terminating decimals – rational numbers that have a finite number of decimal places when written as decimals: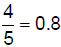
			6.1.4.3.4. repeating decimals – rational numbers that have an infinite number of decimal places filled by the same number or a fixed number of digits repeated over an infinite number of decimal places:
				6.1.4.3.4.1.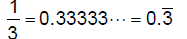
				6.1.4.3.4.2.
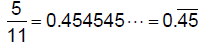				6.1.4.3.4.3. Generalization about decimals for rational numbers: Every rational number can be expressed as a terminating or a repeating decimal
	6.1.5. Problems and Exercises p. 311
		6.1.5.1. Home work: 1-3, 7, 8ac, 9abc, 10c, 11, 12, 14, 19, 20, 22

Your Math Help is on the Way!

More Math Help

Rational Number Ideas and Symbols