Algebra I

Prerequisite Material

Before taking an Algebra I course, students should understand and be able to apply basic
properties of real numbers (i.e. commutative, associative, distributive properties…), be
able to add, subtract, multiply, and divide integers, fractions, and decimals, convert from
one form of a number to another, understand and apply the order of operations rules,
understand and simplify numerical exponential expressions, have a working
understanding of percents, understand the concepts of variables, expressions, and
equations, solve simple linear equations in one variable, and use ratios and proportions to
solve problems.

Required Material

1. Number Systems

a. Counting Numbers, Whole Numbers, Integers, Rational Numbers,
Irrational Numbers, Real Numbers (MA.A.1.4, MA.A.2.4.2, MA.A.3.4.1,
MA.A.3.4.3)
b. Properties of Real Numbers (MA.A.1.4, MA.A.2.4.2, MA.A.3.4.2,
MA.A.3.4.3)

2. Variables and Expressions

a. Terminology such as variable, algebraic expression, exponential
expression, constant, coefficient, opposite, absolute value, and like terms
b. Simplifying variable expressions such as,

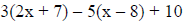
c. Evaluating expressions such as,

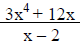for x=-3

3. Solving Linear Equations in One Variable (MA.A.4.4)

a. One-step equations
b. Multi-step equations
c. Equations with variable on both sides of the equal sign
d. Solving a variety of problems including percent problems
e. Solving formulas for specified variables

4. Solving and Graphing Inequalities in One Variable

a. Simple Inequalities (The complexity of these should be consistent with
that of the linear equations that students have learned to solve.)
b. Compound Inequalities

5. Two Variable Functions and their Graphs

a. Relations
b. Functions
c. Different ways of representing functions
d. Graphs of functions
e. An introduction to both linear and nonlinear functions
f. Qualitative graphing

6. Linear Functions in two Variables

a. Slope
b. Intercepts
c. Forms of linear equations (standard, slope-intercept, point-slope)
d. Scatter plots and lines of best fit
e. Direct variation

7. Systems of Two Equations in Two Unknowns

a. Solutions of systems
b. Solving by graphing
c. Solving by substitution
d. Solving by elimination
e. Using systems to solve problems

8. Linear Inequalities in Two Variables and Systems of Linear Inequalities

a. Graphs of linear inequalities and their solutions
b. Graphs of systems of linear inequalities and their solutions
c. Linear programming

9. Equations and Inequalities Involving Absolute Value

a. Solving equations involving absolute value
b. Graphing functions involving absolute value
c. Conjunctions
d. Disjunctions

10. Quadratic Equations

a. Simplifying square root expressions involving both numbers and variables
b. Graphing quadratic functions and identifying their vertices, intercepts, and
lines of symmetry
c. Solving quadratic equations by factoring, taking square roots, and the
quadratic formula
d. Scatter plots and quadratic functions as models

11. Polynomials

a. Multiplying and dividing monomial expressions containing integer
exponents
b. Adding and subtracting polynomials
c. Scientific notation
d. Multiplying polynomials
e. Factoring polynomials
f. Solving quadratic equations by factoring

12. Rational Expressions and Equations

a. Simplifying rational expressions
b. Multiplying and dividing rational expressions
c. Adding and subtracting rational expressions
d. Solving equations with rational expressions
e. Solving problems involving indirect variation

13. Radical Expressions and Right Triangles

a. Simplifying, adding, subtracting, and multiplying square root expressions
(MA.A.1.4.1, MA.A.3.4.3
b. Rationalizing denominators
c. Solving equations with square roots
d. The Pythagorean Theorem
e. The distance formula
f. The midpoint formula
g. Solving similar triangle problems
h. Right triangle trigonometry

14. Probability

a. Combinations, permutations, and sample spaces
b. Compute simple probabilities

15. Data Analysis

a. a. Tables and graphs
b. Distributions and their shapes
c. Measures of center (mean, median, and mode)
d. Measures of spread (range, interquartile range, variance, standard
deviation)
e. Outliers
f. Samples and populations

Other Considerations

• There should be an emphasis on the understanding of the underlying concepts.

• Communication, both oral and written, should be emphasized throughout the
course. Written solutions to problems should be expected and evaluated.

• Students should be allowed to use calculators and computers where appropriate.*

• Classroom activities should be student-centered and involve active/experiential
learning.*

• There should be an emphasis on problem-solving, estimation, and real-world
applications.*

• Alternative assessment should be incorporated into student evaluation.*

• At the end of each semester, a summary of the mathematics covered should occur
in which the relationships among concepts are emphasized. Semester exams are
required of all students.

*Taken from the Florida Department of Education Basic Assumptions for Mathematics
Education.