Algebraic Symmetries
Algebraic Symmetries I
Just as we can factor
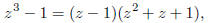
we can factor
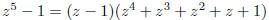
It follows that each of the four numbers
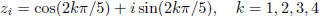
satisfies the equation
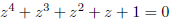
Thus our algebraic interpretation of the five vertices of
the regular pentagon
as the five fifth roots of unity has destroyed the five-fold symmetry. We have
distinguished one vertex, placing it at the point 1=1+0i. So we now have to
look for a different kind of symmetry, that among the four remaining vertices,
or better the four remaining roots.
There is a one obvious symmetry, that which interchanges
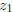 and
and 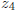 as
as
well as 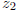 and
and
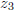 . This is an algebraic as well as an geometric symmetry
. This is an algebraic as well as an geometric symmetry
because it is just a matter of replacing each of the numbers by its complex
conjugate
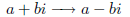
and

I take it as obvious that the complex conjugate of the sum
or the difference of
two complex numbers is the sum or the difference of their complex conjugates.
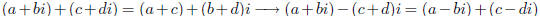
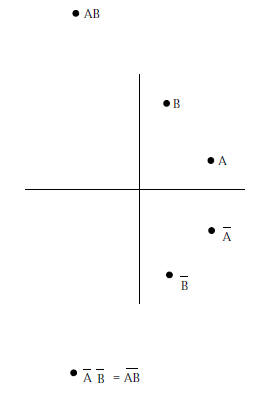
In other words the operation of complex conjugation that
interchanges 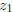 and
and
 as well as
as well as 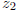 and
and 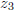

is like reflection in a mirror. All arithmetic properties are faithfully preserved.
Small remarks
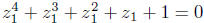
is the same as
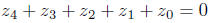
Why is, for example, 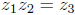 ?
?
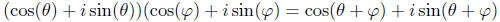
Take 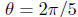 and
and
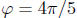 . Then
. Then 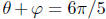 and this becomes
and this becomes
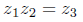
One shows in the same way that, for example, 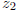
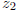 =
= 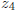 .
Observe
.
Observe
also that, along the same lines,
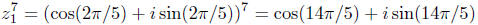
and
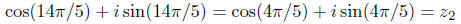
This is because the angle
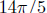 is equal to
is equal to
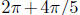 and
the cosine
and
the cosine
and sine do not change when 2π is added to or subtracted from an
angle. Indeed, in some respects, the angle itself does not change!
(Note: this statement is correct, but calls for some reflection!)
Algebraic Symmetries II
This is because i is just a symbol that stands for the
square root of −i
and −i is then introduced and defined by the condition that
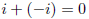
But −i is also just a symbol and can be taken as the
primary symbol. Then
i is a second symbol that functions as −(−i). Even if i is taken to have some
meaning beyond that of a mere symbol, it cannot have a different meaning
than −i, so that the two have to be regarded as perfectly interchangeable.
Are there other symmetries of this kind?
Whether there are other symmetries of this kind affecting
all complex
numbers is not a question for us, but we can ask whether there are symmetries
of this kind affecting just 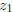 ,
, 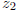 ,
, 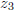 and
and 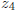 . Before we do, we make use of the
. Before we do, we make use of the
symmetry at hand. Since 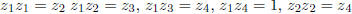 ,
,
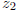
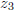 = 1 and so on, and since in addition
= 1 and so on, and since in addition
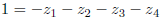
the numbers
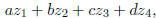
where a, b, c and d are arbitrary ordinary fractions form
a collection closed
under addition, subtraction, multiplication, and even as it turns out division.
The numbers that are equal to their own reflections can be singled out. These
are the numbers
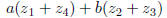
The appearance of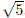 .
.
Let w be the number 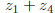 .
It is equal to its own reflection. So is its
.
It is equal to its own reflection. So is its
square. Thus
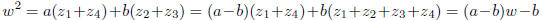
Thus w satisfies a quadratic equation

We calculate this equation
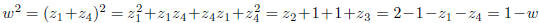
Thus
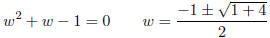
Since w is a positive number,
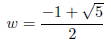
In other words, w can as we know be constructed with ruler
and compass.
Since
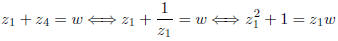
we have
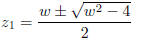
Since 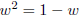 , this is
, this is
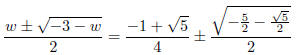
Since 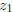 lies above the axis of abscissas,
lies above the axis of abscissas,
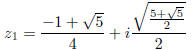
Symmetries III
Having found 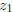 , we can easily find
, we can easily find 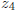 , its complex conjugate, and we can
certainly
, its complex conjugate, and we can
certainly
find 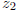 by squaring
by squaring 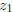 . We can also
find
. We can also
find 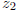 by working with
by working with 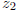 +
+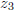 rather than w.
This is,
rather than w.
This is,
however, straightforward algebra. As Descartes insisted, the algebra often turns
a problem
into an almost unthinking manipulation of symbols, a turn that it can indeed
often take,
but we prefer another direction. This is the direction taken by Gauss.
Let 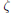 be the number
be the number 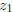 . Then
. Then 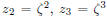 , and
, and
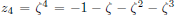
because

Our numbers 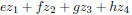 can also be
expressed as
can also be
expressed as
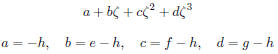
Are these numbers all different?
This is an important question! The answer is yes and I shall give a proof
following
Gauss. We first note the consequences. Since the numbers are all different, we
cannot have
an equation
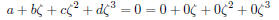
unless a = b = c = d = 0. This means that
![]() satisfies the
equation
satisfies the
equation

and essentially only this equation, because if we have any other such as
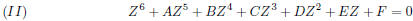
then by the process of long division we will have
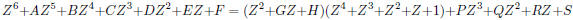
so that
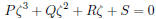
We have just seen that this implies P = Q = R = S = 0. Thus
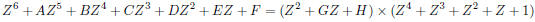
and (II) is a consequence of (I).


