Model Academic Standards for Mathematics
Glossary of Terms
Algorithm. An established step-by-step procedure
used to achieve a
desired result. For example, the addition algorithm for the sum of two
two-digit numbers where carrying is required:
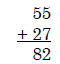
Arbitrary unit (of measure). A unit that is not
part of the standardized metric or US
Customary systems. For example, using one’s own shoe size to measure the length
of a door
opening or saying that the area of an exhibition hall floor is “about the size
of two football
fields.”
Associative property. When adding or multiplying
three numbers, it doesn’t matter if the
first two or the last two numbers are added or multiplied first. For example,
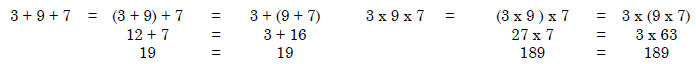
Attribute (measurable). An identifiable property of
an object, set, or event that is subject
to being measured. For example, some of the measurable attributes of a box are
its length,
weight, and capacity (how much it holds).
Box plot. A graphic method that shows the
distribution of a set of data by using the
median, quartiles, and the extremes of the data set. The box shows the middle 50
percent of
the data; the longer the box, the greater the spread of the data.
Central tendencies. A number which in some way
conveys the “center” or “middle” of a
set of data. The most frequently used measures are the mean and the median.
Combinations. Subsets chosen from a larger set of
objects in which the order of the items
in the subset does not matter. For example, determining how many different
committees of
four persons could be chosen from a set of nine persons. (See also,
Permutations)
Commutative property. Numbers can be added or
multiplied in either order. For
example, 15 + 9 = 9 + 15; 3 x 8 = 8 x 3.
Congruence. The relationship between two objects
that have exactly the same size and
shape.
Correlation. The amount of positive or negative
relationship existing between two
measures. For example, if the height and weight of a set of individuals were
measured, it
could be said that there is a positive correlation between height and weight if
the data
showed that larger weights tended to be paired with larger heights and smaller
weights
tended to be paired with smaller heights. The stronger those tendencies, the
larger the
measure of correlation.
Deciles. The 10th, 20th, 30th, ...90th percentile points. (See definition for Percentile)
Direct measurement. A process of obtaining the
measurement of some entity by reading a
measuring tool, such as a ruler for length, a scale for weight, or a protractor
for angle size.
Dispersion. The scattering of the values of a
frequency distribution (of data) from an
average.
Distributive property. Property indicating a
special way in which multiplication is
applied to addition of two (or more) numbers. For example,
5 x 23 = 5 x (20 + 3) = 5 x 20 + 5 x 3 = 100 + 15 = 115.
Expanded notation. Showing place value by
multiplying each digit in a number by the
appropriate power of 10. For example, 523 = 5 x 100 + 2 x 10 + 3 x 1 or 5 x 102
+ 2 x 101 + 3
x 100.
Exponential function. A function that can be represented by an equation of the
form
y = abx + c, where a, b, and c are arbitrary, but fixed, numbers and a ≠ 0 and b
> 0 and b ≠ 1.
Exponential notation (exponent). A symbolic way of showing how many times a
number
or variable is used as a factor. In the notation 53, the exponent 3 shows that 5
is a factor
used three times; that is 53 = 5 x 5 x 5 = 125.
Frequency distribution. An organized display of a set of data that shows how
often each
different piece of data occurs.
Function. A relationship between two sets of numbers or other mathematical
objects
where each member of the first set is paired with only one member of the second
set.
Functions can be used to understand how one quantity varies in relation to (is a
function of)
changes in the second quantity. For example, there is a functional relationship
between the
price per pound of a particular type of meat and the total amount paid for ten
pounds of
that type of meat.
Functional notation. A convenient way to show how a function takes a value and
transforms it into a new value. A commonly used notation is called Euler
notation and is
written f (x) and read “f of x.” For example, if f (x) = 3x + 5, this means that
the function f
will take any value from the domain of x and multiply it by 3 and then add 5 to
make the
new value for x (e.g., f (4) = 3*4 + 5 = 17).
Identity. For addition: The number 0; that is N + 0 = N for any number N. For
multiplication: The number 1; that is, N x 1 = N for any number N.
Indirect measurement. A process where the measurement of some entity is not
obtained
by the direct reading of a measuring tool or by counting of units superimposed
alongside or
on that entity. For example, if the length and width of a rectangle are
multiplied to find the
area of that rectangle, then the area is an indirect measurement.
Integers. The set of numbers: {..., -6, -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, 6,...}
Intercept. The points where a line drawn on a rectangular-coordinate-system
graph
intersect the vertical and horizontal axes.
Inverse. For addition: For any number N, its inverse (also called opposite) is a
number -N
so that N + (-N) = 0 (e.g., the opposite of 5 is -5, the opposite of -3/4 is
3/4).
For multiplication: For any number N, its inverse (also called reciprocal) is a
number N* so
that N x (N*) = 1 (e.g., the reciprocal of 5 is 1/5; the reciprocal of -3/4 is
-4/3).
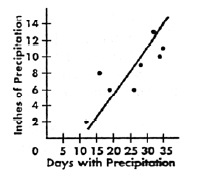
Line of best fit. A straight line used as a best
approximation of a summary of all the points in a
scatter-plot* (See definition below). The position and
slope of the line are determined by the amount of
correlation* (See definition above) between the two
paired variables involved in generating the scatter-plot.
This line can be used to make predictions about the
value of one of the paired variables if only the other
value in the pair is known
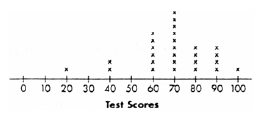
Line plot. A graphical display of a set of data where
each separate piece of data is shown as a dot or mark
above a number line.
Linear equation. An equation of the form y = ax + b, where a and b can be any
real
number. When the ordered pairs (x, y) that make the equation true for specific
assigned
values of a and b are graphed, the result is a straight line.
Matrix (pl.: matrices). A rectangular array of numbers, letters, or other
entities arranged
in rows and columns.
Maximum/minimum (of a graph). The highest/lowest point on a graph. A relative
maximum/minimum is higher/lower than any other point in its immediate vicinity.
Mean. The arithmetic average of a set of numerical data.
Median. The middle value of an ordered set of numerical data. For example, the
median
value of the set {5, 8, 9, 10, 11, 11,13} is 10.
Mode. The most frequently occurring value in a set of data. For example, the
mode of the
set {13, 5, 9, 11, 11, 8, 10} is 11.
Model (mathematical). A [verb] and a noun. [Generate] a mathematical
representation
(e.g., number, graph, matrix, equation(s), geometric figure) for real-world or
mathematical
objects, properties, actions, or relationships.
(Non)-Linear functional relationship. (See definition of Function above.) Many
functions can be represented by pairs of numbers. When the graph of those pairs
results in
points lying on a straight line, a function is said to be linear. When not on a
line, the
function is nonlinear.
Nonroutine problem. A problem is nonroutine if it cannot be solved simply by
substituting specific data into a formula that the student knows, or by
following step-bystep
the solution of a type of problem with which the student is already familiar.
Outlier. For a set of numerical data, any value that is markedly smaller or
larger than
other values. For example, in the data set {3, 5, 4, 4, 6, 2, 25, 5, 6, 2} the
value of 25 is an
outlier.
Patterns. Recognizable regularities in situations such as in nature, shapes,
events, sets of
numbers. For example, spirals on a pineapple, snowflakes, geometric designs on
quilts or
wallpaper, the number sequence {0, 4, 8, 12, 16,...}.
Percentile. A value on a scale that indicates the percent of a distribution that
is equal to it
or below it. For example, a score at the 95th percentile is equal to or better
than 95 percent
of the scores.
Permutations. Possible arrangements of a set of objects in which the order of
the
arrangement makes a difference. For example, determining all the different ways
five books
can be arranged in order on a shelf.
Prime number. A whole number greater than 1 that can be divided exactly (i.e.,
with no
remainder) only by itself and 1. The first few primes are 2, 3, 5, 7, 11, 13,
17, 19, 23, 29, 31,
37….
Pythagorean theorem (relationship). In a right triangle, c2 = a2 + b2, where c
represents
the length of the hypotenuse (the longest side of the triangle which is opposite
the right
angle), and a and b represent the lengths of the other two, shorter sides of the
triangle.
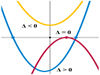
Quadratic function. A function that can be represented by an equation of the
form y = ax2
+ bx + c, where a, b, and c are arbitrary, but fixed, numbers and a ≠ 0. The
graph of this
function is a parabola.
Quartiles. The 25th, 50th and 75th percentile points. (See definition of Percentile.)
Range (of a set of data). The numerical difference between the largest and
smallest values
in a set of data.
Rational number. A number that can be expressed as the ratio, or quotient, of
two
integers, a/b, provided b ≠ 0. Rational numbers can be expressed as common
fractions or
decimals, such as 3/5 or 0.6. Finite decimals, repeating decimals, mixed numbers
and whole
numbers are all rational numbers. Nonrepeating decimals cannot be expressed in
this way,
and are said to be irrational.
Real numbers. All the numbers which can be expressed as decimals.
Real-world problems. Quantitative and spatial problems that arise from a wide
variety of
human experiences, applications to careers. These do not have to be highly
complex ones
and can include such things as making change, figuring sale prices, or comparing
payment
plans.
Rectangular coordinate system. This system uses two (for a plane) or three (for
space)
mutually perpendicular lines (called coordinate axes) and their point of
intersection (called
the origin) as the frame of reference. Specific locations are described by
ordered pairs or
triples (called coordinates) that indicate distance from the origin along lines
that are
parallel to the coordinate axes.
Scaling (Scale drawing). The process of drawing a figure either enlarged or
reduced in
size from its original size. Usually the scale is given, as on a map 1 inch
equals 10 miles.
Scatter plot. Also known as scattergram or scatter diagram. A
two dimensional graph representing a set of bi-variate data.
That is, for each element being graphed, there are two separate
pieces of data. For example, the height and weight of a group of
10 teenagers would result in a scatter plot of 10 separate points
on the graph.
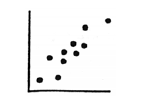
Scientific notation. A short-hand way of writing very large or very small
numbers. The
notation consists of a decimal number between 1 and 10 multiplied by an integral
power of
10. For example, 47,300 = 4.73 x 104; 0.000000021 = 2.1 x 10-8.
Similarity. The relationship between two objects that have exactly the same
shape but not
necessarily the same size.
Simulation. Carrying out extensive data collection with a simple, safe,
inexpensive, easyto-
duplicate event that has essentially the same characteristics as another event
which is of
actual interest to an investigator. For example, suppose one wanted to gather
data about
the actual order of birth of boys and girls in families with five children
(e.g., BBGBG is one
possibility). Rather than wait for five children to be born to a single family,
or identifying
families that already have five children, one could simulate births by
repeatedly tossing a
coin five times. Heads vs. tails has about the same chance of happening as a boy
vs. a girl
being born.
Slope. A measure of the steepness or incline of a straight line drawn on a rectangularcoordinate-
system graph. The measure is obtained by the quotient “rise/run” (vertical
change divided by horizontal change) between any two points on that line.
Stem-and-leaf plot. A way of showing the distribution of a
set of data along a vertical axis. The plot at right shows the
data 13, 19, 33, 26, 19, 22, 34, 16, 28, 34. The ten’s digits of
these data are the stems and the one’s digits are the leaves.
1|3699
2|268
3|344
Key: 1|5 means 15
Summary statistics. A single number representation of the characteristics of a
set of data.
Usually given by measures of central tendency and measures of dispersion
(spread).
Symmetry. A figure has symmetry if it has parts that correspond with each other
in terms
of size, form, and arrangement. For example, a figure with line (or mirror)
symmetry has
two halves which match each other perfectly if the figure is folded along its
line of
symmetry.
Transformation. A change in the size, shape, location or orientation of a figure.
Transitive property. For equality: If a = b and b = c, then a = c.
For inequality: If a > b and b > c, then a > c; or If a < b and b < c, then a <
c.
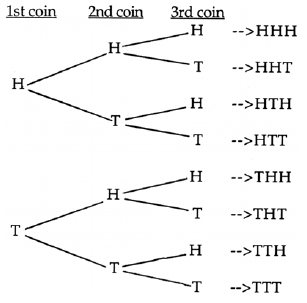
Tree diagram. A schematic way of showing the
number of ways a compound event may occur.
For example, the tree diagram at the right shows
the eight possible ways the tossing of three coins
could happen.
Unit fraction. A fraction with a numerator of 1, such as 1/4 or 1/7.
Variable. A quantity that may assume any one of a set of values. Usually
represented in
algebraic notation by the use of a letter. In the equation y = 2x + 7, both x
and y are
variables.
Variance. The value of the standard deviation squared.
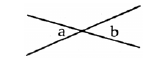
Vertical angles. The pair of angles that are directly
across from each other when two straight lines
intersect. Angles a and b at the right are an example of
vertical angles.
Whole numbers. The numbers: 0, 1, 2, 3, 4, 5,….