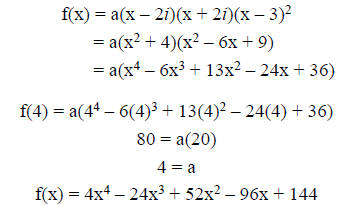Division of Polynomials
Divide: 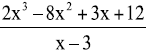
|
Division of Polynomials 1. Divide 1st term by 1st term 2. Multiply 3. Subtract 4. Repeat |
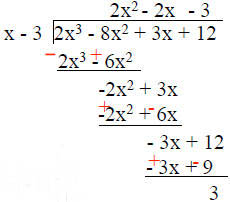 |
| Quotient: 2x2 - 2x - 3 Remainder: 3 |
Synthetic Division
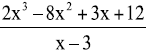
| 1. For a divisor of x - c, use c 2. Write coefficients of dividend 3. Add down 4. Multiply up |
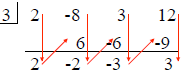 |
| Quotient: 2x2 - 2x - 3 Remainder: 3 |
For any polynomial f(x) and any complex number k,
there exists a unique polynomial q(x) and number r such
that f(x) = (x - k)q(x) + r
Division: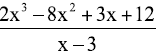 |
Quotient: 2x2 - 2x - 3 Remainder: 3 |
Alternate forms
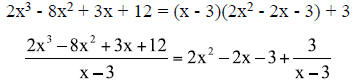
The Remainder Theorem
If r is the remainder when f(x) is
divided by x - c, then f(c) = r
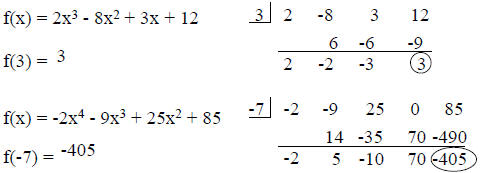
A zero of a polynomial function f(x) is any
number c, such that f(c) = 0.
Decide whether –2 and –3 are zeros of
f(x) = x3 – 7x + 6
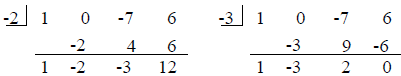
f(–2) = 12, f(–3) = 0
–3 is a zero of the function
A zero of a polynomial function f(x) is any
number c, such that f(c) = 0.
Decide whether 3i is a zero of
f(x) = x4 – 2x3 + 6x2 – 18x – 27
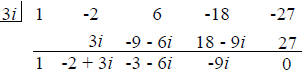
f(3i) = 0
3i is a zero of the function
The Factor Theorem
For any polynomial f(x), x - k is a factor
of f(x) if and only if f(k) = 0.
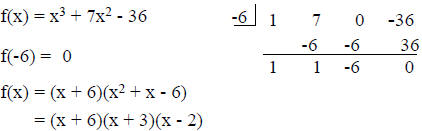
zeros: -6, -3, 2
The Rational Zeros Theorem
If p/q is a zero of a polynomial function f(x), then p is a
factor of the constant term, and q is a factor of the
leading coefficient.
List all possible rational zeros of the function
f(x) = 2x3 – 3x2 – 11x + 6
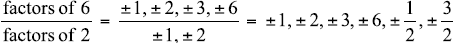
Find the rational zeros and factor
f(x) = 2x3 – 3x2 – 11x + 6
Possible rational zeros: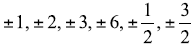
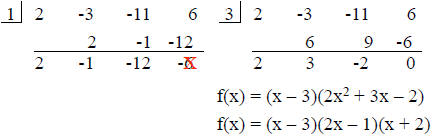
zeros: 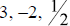
Fundamental Theorem of Algebra
Every polynomial of degree n, where n ≥ 1, has at
least one complex zero.
Number of Zeros Theorem
A polynomial of degree n has at most n distinct zeros.
Combined Result
A polynomial of degree n has exactly n complex zeros,
possibly not all distinct.
Example: f(x) = x3 – 3x + 2 = (x + 2)(x – 1)(x – 1)
f(x) has degree 3, and has exactly 3 zeros: –2, 1, 1
1 is called a zero of multiplicity 2 since it occurs twice.
Conjugate Zeros Theorem
If f(x) is a polynomial having only real coefficients, and
if a + bi is a zero of f(x), then a – bi is also a zero of f(x).
f(x) = x2 – 2x + 5
zeros: x2 – 2x + 5 = 0
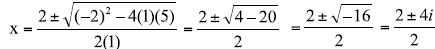
zeros: 1 + 2i, 1 – 2i
Find a polynomial of lowest degree with real coefficients
having zeros 2i, and 3 (multiplicity 2), for which f(4) = 80.