Polynomials
In this section we want to review all that we know about
polynomials.
We start with the basic operations on polynomials, that is adding, subtracting,
and multiplying.
Recall, to add or subtract polynomials we simply combine like terms. To multiply
polynomials we
have to multiply each term in the first polynomial by each term in the second
polynomial and
combine like terms. When multiplying two binomials we can use the FOIL method
(First-Outer-
Inner-Last).
Example 1:
Perform the following operations

Solution:
a. Since the parentheses are not needed in this expression, we can simply
combine like
terms.
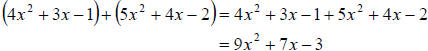
b. This time we need to start by distributing the
negative. Then we combine like terms.
We get
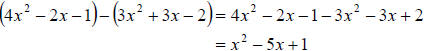
c. To multiply these two binomials we will simply multiply
each term in the first binomial by
each term in the second binomial and combine like terms. We get
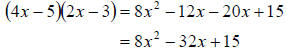
d. Lastly, we again multiply each term in the first
polynomial by each term in the second
polynomial and combine like terms. We get
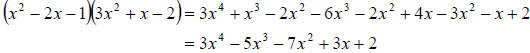
Next we want to review basic factoring of polynomials.
There are four types of factoring we want
to review: factoring the GCF, factor by grouping, factor by trial factors,
factoring by formula.
The technique we use for factoring is as follows.
| General Strategy for Factoring |
| 1. Factor out the GCF. 2. Count the number of terms in the remaining polynomial. If it has a. Four terms- we factor by grouping b. Three terms- we factor by trial factors c. Two terms- we use one of the following factoring formulas 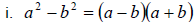 , called the difference of squares , called the difference of squares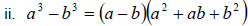 , called the difference of cubes , called the difference of cubes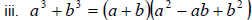 , called the sum of cubes , called the sum of cubes3. Check each factor to see if you can factor it further. If so, then we factor again. |
Example 2:
Factor completely.
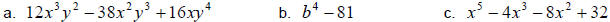
Solution:
a. We start by factoring out the GCF, which is clearly 2xy2. We get
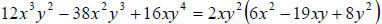
We see that we are left with a three term polynomial (a
trinomial). So we factor by trial
factors. That is, we know that every trinomial
that factors, will factor as two binomials.
So we simply guess at the way it
factors and check by multiplying it back out. Some of
the key ideas are the
first terms in each binomial will have to have a product that is the
leading
term of the trinomial and the second terms in each binomial will have to have a
product that is the last term of the trinomial. So by trial factors we get
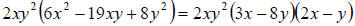
b. Since we can see there is clearly no GCF here we can
begin by counting the terms.
Since we have two terms we are going to have to
factor by a formula. Clearly our only
choice is the difference of squares. So we
will make each term into a square as follows.
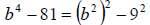
Now we use the formula to factor. This gives
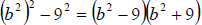
Now we need to check each factor to see if we can do more
factoring. We see that the
first binomial is again a difference of squares.
Therefore we must factor it again. We get
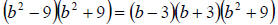
We cannot factor a sum of squares, therefore the
expression is completely factored.
c. Lastly, we see no GCF so we can start by factoring by grouping. That is, we
group
together the first two terms and the last two terms and factor what we can
out of those
pairs. Then we see if there is a common binomial factor. If not we
try grouping another
way. We proceed as follows
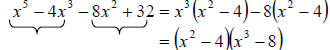
Now we check to see if there is more factoring to be done.
Clearly the first binomial is
the difference of square and the second binomial
is the difference of cubes. So we factor
with the formulas given above. We get
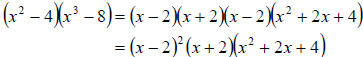
Since the trinomial does not factor, the expression is
completely factored.
Factoring polynomials leads us directly to solving polynomial equations. To do
this we use the
following property.
| Zero Product Property |
If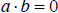 , then , then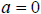 or
or 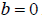 . . |
So to solve a polynomial equation, we get one side of the
equation to be zero, factor completely,
set each factor to zero and continue
solving.
Example 3:
Solve
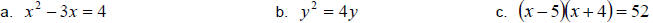
Solution:
a. We start by getting a zero on one side and factoring completely. This gives
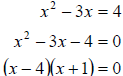
Now, according to the zero product property we can set
each factor to zero. We can then
finish solving. We get
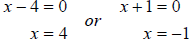
So the solution set is 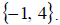
b. Again we start by getting a zero on one side and factoring. We then set each
factor to
zero and solve. We have
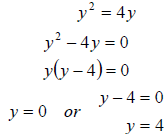
So the solution set is 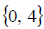
c. This time we need to start by multiplying out the
binomials, then we can proceed as
usual. We get
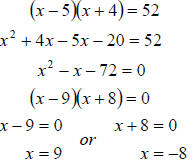
So the solution set is 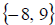 .
.
Lastly, we want to do some word problems which require us to use polynomials.
Example 4:
A certain graphing calculator is rectangular in shape. The length of the
rectangle is 2 cm more
than twice the width. If the area of the calculator is
144 cm0, what are the length and width of the
calculator?
Solution:
First we should draw a picture to represent the situation. Since the length of
the rectangle is 2 cm
more than twice the width we have
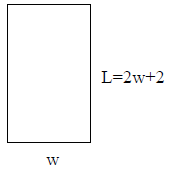
Since we know that the area of a rectangle is
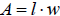 we have
we have
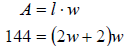
Now that we have an equation, we simply need to solve it.
We
get
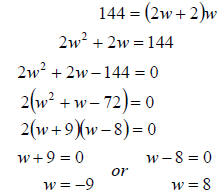
Since w is the width of a rectangle, it cannot be
negative. Thus, w=8. Now we can simply find
l. Since l = 2w + 2, l = 2(8) + 2 =
18.
So the calculator is 8 cm by 18 cm.
Example 5:
The formula for the number of games to be played in a soccer league where each
team is to play
each other twice is 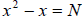 , where x
is the number of teams in the league and N is the
, where x
is the number of teams in the league and N is the
number of games to be played.
If a league wants to limit the games to a total of 132 games, how
many teams can
be in the league?
Solution:
For this example we are given a formula which we must interpret. Since N is the
number of
games to be played and we want a total of 132 games, N = 132. Putting
that into the formula we
get an equation we can solve.
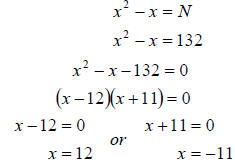
Since x represents the number of teams, it cannot be
negative. Therefore, the league must have
12 teams to play a total of 132 games.
R.4 Exercises
Perform the indicated operations.
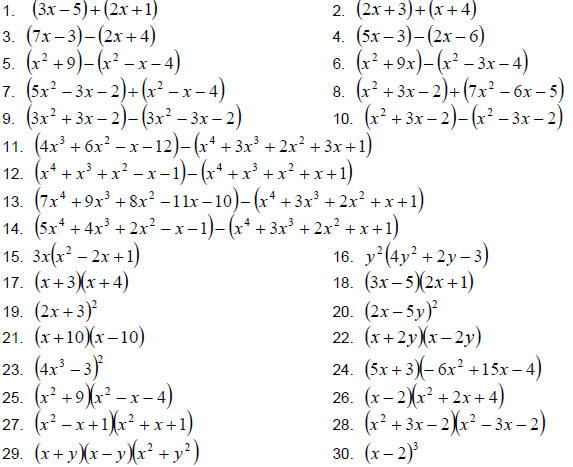
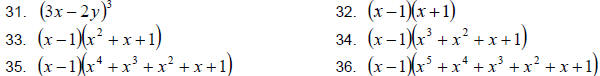
Factor completely.
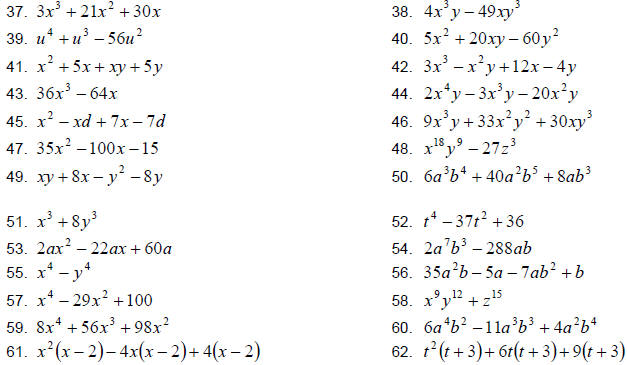
Solve the following.

73. The length of a rectangle is 2 meters less than 2
times the width. The area is 24 square
meters. Find the dimensions.
74. The width of a rectangle is 5 feet less than 4 times the length. The area is
21 square feet.
Find the dimensions.
75. The length of a rectangle is 2 inches more than 3 times the width. The area
is 33 square
inches. Find the dimensions.
76. The area of a triangle is 30 square feet. The height is 11 feet less than
the base. Find the
dimensions.
77. The area of a triangle is 39 square meters. The height is 7 meters more than
the base. Find
the dimensions.
78. The area of a triangle is 35 square inches. The base is 9 inches less than
the height. Find the
dimensions.
Find the time it takes the object to hit the ground, where h is in feet, and t is in seconds.
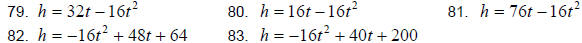
84. A ball rolls down a slope and travels a distance
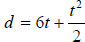 feet in t seconds. Find t when
feet in t seconds. Find t when
d is 14 feet .
85. A ball rolls down a slope and travels a distance
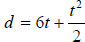 feet in t seconds. Find t when
feet in t seconds. Find t when
d is 32 feet.


