MATH 120 Exam 3 Information

1. Know how to solve linear and quadratic equations from Chapter 1. These arise in various
contexts related to Chapter 3. For example, solve for x:

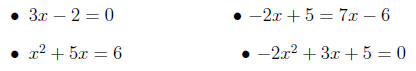
2. Find and simplify the difference quotient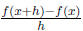for a function f(x):

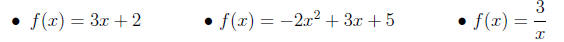
3. Find the inverse of a function:

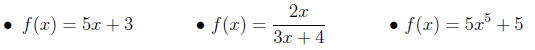
4. For a quadratic function, identify (a) the direction of opening, (b) the vertex, (c) the axis
of symmetry, (d) the domain, and (e) the range.

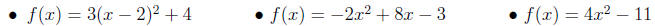
5. Find the formula for a quadratic function f(x) which satisfies various properties. E.g.,

 •Vertex at (-1,-2), opening upward, having the same shape as g(x) = 4x^2 - 9x + 7
 •Having a relative maximum at (4, 3) and the same shape as g(x) = x^2.

6. Be able to solve a word problem involving quadratic functions such as:

 •The pro t (in dollars) a company makes from producing and selling x widgets is p(x) =
-3x^2 + 24x - 36. For what range of x-values is the pro t at least zero? How many
should be sold to have a pro t of $10? How many should be sold to have the largest
pro t? What is that profit?

 •A rectangular office area is to be made which will contain six adjacent cubicles. The
width of each cubicle will be the same but the lengths do not need to be. The material
for the back of the cubicles will cost $20 per linear foot, the material for the sides (the
"widths") will cost $10 per linear foot, and the material for the front of the cubicles will
cost $50 per linear foot. The company has $3360 to spend. What should the overall
dimensions of the total complex be in order to maximize the total enclosed area?

7. Be able to identify the end behavior of a polynomial function. E.g.

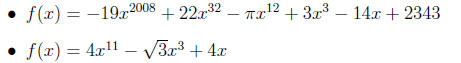
8. Be able to perform long division of polynomials. This could be alone or in the context of another problem. E.g.

9. Be able to perform synthetic division. This could be alone or in the context of another problems. E.g.

10. Be able to use the Rational Zero Theorem to list all possible rational zeros for a given function. E.g.

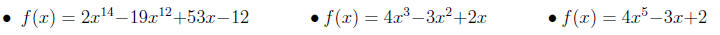
11. Find all zeros of a polynomial function. Include complex zeros. E.g.

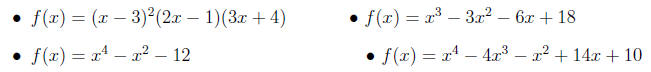
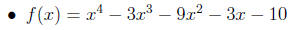knowing that -i is a zero

12. Find formulas for polynomial functions. E.g.

 •f(x) has degree three, zeros of 2 and 3 - i, and f(0) = 8.
 •f(x) has degree four, zeros of 1 and -1 both of multiplicity two, and f(2) = 7.

13. Be able to solve a polynomial inequality. E.g.

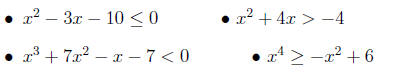
14. Be able to solve a rational inequality. E.g.

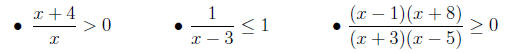
15. As with the previous exams, you should be prepared for some short answer, true-false,
give an example sort of questions on topics from the chapter. E.g. (but not inclusive), identifying
whether something is a polynomial, identifying the degree of a polynomial, determining
the multiplicity of a zero, giving an example of some sort of polynomial, ...

16. General suggestions: Go over the online and paper homeworks, especially problems
you had difficulty with. If you like the online system, under the "Tests" category, there are
pre-made chapter tests for Chapter 1 which you might want to try. You can also use the
Study plan which will generate sample problems for you for each section.

17. Details: The exam is worth 100 points. There will be 12 to 17 questions worth varying
amounts of credit. E.g., some more involved problems will be worth more. No notes or books
are allowed. You may have a calculator.