Final Review Solutions

ADVICE: Attempt to do all problems without referring to your notes or
the book. Then, if you get stuck, look at your notes, then attempt to do it
again later without your notes. Also, rework all the old tests, again trying
not to look at your notes or solutions.

(1) Determine whether the following function is even, odd or neither:

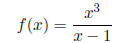
Solution: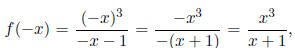so f is neither even nor odd.

(2) For the function h(x) = 4x² - 3x + 1 determine:
(a) the average rate of change from 1 to 3
Solution: Use the formulaSo,

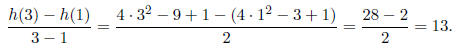
(b) the equation of the secant line through (1, h(1)) and (3, h(3)).
Solution: You must first find m_sec using part i). So, m_sec = 13. Pick
either point and use the point slope formula:

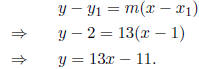
(3) Suppose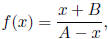 f(90) = 0 and f(16) is undefined. Determine A and B.

Solution:
f is 0 where the numerator is 0, and f is undefined where the
denominator is 0. So, you are given that f(90) = 0, which means
the numerator is 0 at 90, i.e.,
90 + B = 0 ==> B = −90.

You are given that f(1) is undefined, which means the denomi-
nator is 0 at 1, i.e.,
A - 16 = 0 ==> A = 16.

(4) Determine the following for

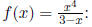
(a) Are the points (2, 16), (1, 0) on the graph of f?
Solution: (2, 16) is, because 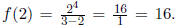(1, 0) is not, be-cause

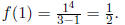
(b) if x = 4, what is f(x)?

Solution: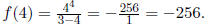

(c) if f(x) = 0, what is x?

Solution: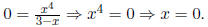

(d) what is the domain of f?
Solution: A fraction is undefined where the denominator is 0. Thus, if
3 − x = 0 ==> x = 3 then f is undefined. So, the domain is
R − {3}

(5) - 10 pts. Suppose the function f is defined by f(x) = −x³.

(a) Determine the function that results from shifting f right by 7.
Graph it.
Solution: −(x − 7)³

(b) Determine the function that results from shifting the function
from part (a) vertically by -5 units. Graph it.
Solution: −(x − 7)³− 5

(6) For 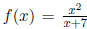determine the slope of the secant line, m_sec. What
value does m_sec approach as h approaches 0?

Solution: To compute the slope of the secant line use the difference quotient

which is the slope of the secant line. Plugging in h = 0 we se that

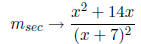
as h → 0.

(7) A wire of length x is bent into the shape of a rectangle.
(a) Express the perimeter of the rectangle as a function of x.

Solution:
P(x) = x.
(b) If the length of the rectangle is twice the width express the area
of the rectangle as a function of x.

Solution: From (a) we have that P(x) = x. Length is twice the width,
so l = 2w. The equation for the perimeter is 2l + 2w =
2l + l = 3l ==> 3l = x. Thus l = x/3 ==> w = x/6. So, the area is

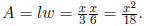
(8) Determine, without graphing, whether the given quadratic function
has a maximum or minumum. Find the value of the max. or min.
g(x) = −5x² − 40x + 9.

Solution: The graph has a maximum because a = −5 < 0, which implies the
graph is pointing down. For any quadratic function, the max/min
occurs at 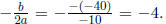 So, the max occurs at −4, so
the maximum is g(−4) = 89

(9) Suppose f(x) = (x − .000004)⁹876(x − 58393)²x⁴000(x + 4).

(a) List the real zeros of f and their multiplicity.
Solution:
x = .000004 has multiplicity 9876.
x = 58393 has multiplicity 2.
x = 0 has multiplicity 4000.
x = −4 has multiplicity 1.

(b) Determine the power function that dictates the behavior of f for
large |x|.
Solution: The power function will have exponent equal to the highest
exponent in the function. If f were expanded out, the highest
exponent would be 9876 + 2 + 4000 + 1 = 13879. Thus,
p(x) = x¹3879 is the corresponding power function.

(10) Find the vertical and horizontal asymptotes of

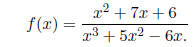
Solution:

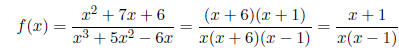
so x = 1 and x = 0 are vertical asymptotes. Now,

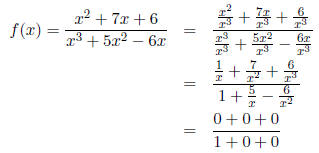
as |x| becomes large, so there is a horizontal asymptote of 0.

(11) Solve the following inequality algebraically:

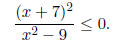
Solution: There is a zero at x = −7. Undefined at x = ±3. So, the intervals
we check are
(−∞,−7) (−7,−3) (−3, 3) (3,∞).

Checking whether positive or negative yields
(−3, 3).

(12) Let f(x) = x³− 90x² + 70 on [0, 1].

(a) Use the Intermediate Value Theorem to show f has a real zero in
[0, 1].
Solution: f(0) is positive and f(1) is negative, so f has a real zero in
(0, 1).

(b) List all the possible zeros in the interval [0, 1].
Solution: p|70 and q|1, so p = ±1,±70,±35,±2,±14,±5,±7,±10 and
q = ±1.
So the possible roots are ±1,±2,±5,±7,±10,±14,±35,±70,
but in (0, 1) we only have 1, 2, 5, 7, 10, 14, 35, 70.

(13) Let f be a complex polynomial of degree 6 with zeros: 18 − i, 12 +
i, −2i. Determine the remaining zeros of f.

Solution: Negate the complex part of each root to yield
18 + i, 12 − i, 2i.

(14) Solve for x:

Solution:

(15) Solve for y:

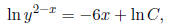
where C is a constant.

Solution:

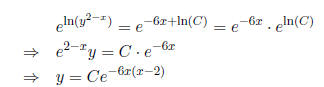
(16) Express as one logarithm:

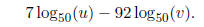
Solution:

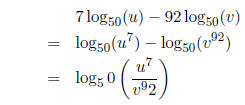
(17) Solve for x:

Solution:

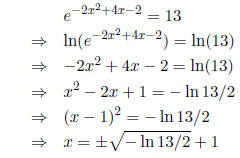
(18) Find the exact value of

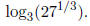
Do not use a calculator.

Solution: Let 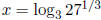Then

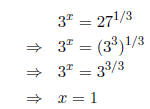
(19) Find the inverse of f(x) = x³and show that it is, in fact, the inverse.
Sketch f and f^--1

Solution: Switch x and y, then solve for y.

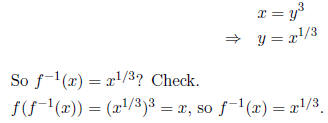
(20) Le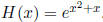t Find f, g such that

f סg(x) = H(x).

Solution: The easiest choice would be

f(x) = e^x
and
g(x) = x² + x.

(21) The half-life of a radioactive material is 290,000 years. If 67 milligrams
are present now, how much will be present in 92,000 years?

Solution:

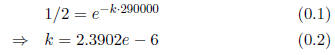
So, plug 92,000 into 67 · e^-2.3902e-6.t to get 53.77 milligrams.

(22) How much money should you ask your brother for if you want to invest
it at 2% compounded continuously, and you want to have $4,000 in 6
months?

Solution:

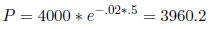
(23) a) Convert 2º to radians.
Solution:

b) Convert π/30 radians to degrees.
Solution:

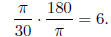
(24) Use Fundamental Trig. Identities or the Complementary Angle Theo-
rem to find the exact value of:

a) csc(12º) csc(78º).

Solution:
csc(12) csc(78) = csc(12) sin(12) = 1
since csc and sin are inverses.

b) csc²(19) + tan²(71).

Solution:
csc²(19) + tan²(71) = csc²(19) + cot²(19) = 1

since
1 − cot²θ = csc²θ

(25) Use the Reference angle of the given angles to find its exact value.

a) tan 4π/3.
Solution: Reference angle is 60, so tan 4π/3 = ±tan 60. Since 4π/3
is in the first quadrant tan 4π/3 = tan 60

b) cos 99.
Solution: Reference angle is 81, so cos 99 = ±cos 81. Since 99 is in the
second quadrant cos 99 = -cos 81.