Pre-Algebra and Algebra Instruction and Assessments
Connecting Arithmetic to Algebra
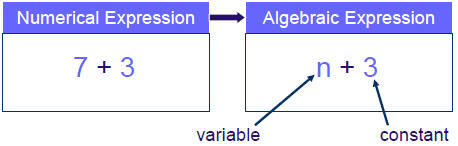
Here is how you read algebraic expressions
| sum | n + 3 “n plus 3” | difference | n – 3 “n less 3” |
| product | 3 x n or 3n “3 times n” | quotient | n÷3 “n divided by 3” |
In the Dog House
Moving from Expressions to
Equations
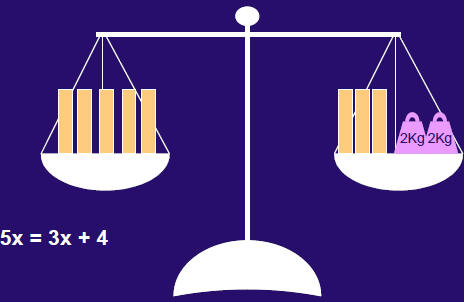
• Problem: The left pan of a set of scales
contains 5 identical boxes of noodles,
and the right pan contains 3 identical
boxes and two 2-kg weights. The scales
are balanced. How much does each box
weigh?
Equation: An equality with a variable.
Root: Each value of the variable that makes the statement a
true equality.
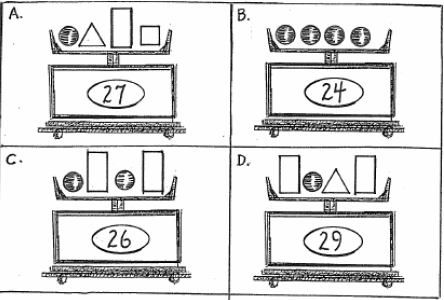
| The scale each part shows the total weight of the
shapes on that scale ,The same shapes have the same weight in each of the pictures, Find the weight of each shape , HINT: You may begin with any one of the four pictures that will help you start. |
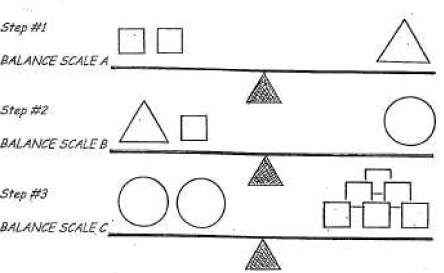
| Give your own values to the figure in A, B, and
C. The same figures in A, B, and C will have the same values ,Different figure will stand for different values ,Remember to keep the scale in A ,B ,and C balanced! |
|
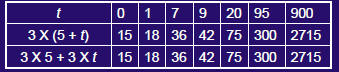
17.Expressions with a variable problem.5 truckloads of sand were x truckloads were delivered. Each truck held 3 tons of sand . How many tons of sand were delivered to the playlot? |
 |
| 5 + t truckloads Each truckload contained 3 tons of sand The total amount of sand delivered is 3 X (5 + t) |
|
| 3 (5 + t) is an expression with a variable If t is 2, than 3 X (5 + 2) = 21 If t is 5, than 3 X (5 + 5) = 30 |
|
Variables and Properties
• A variable represents a number–even
though its value may not be given.
• Expressions with variables satisfy all the
properties of the number system, such
as the commutative, associative, and
distributive properties.
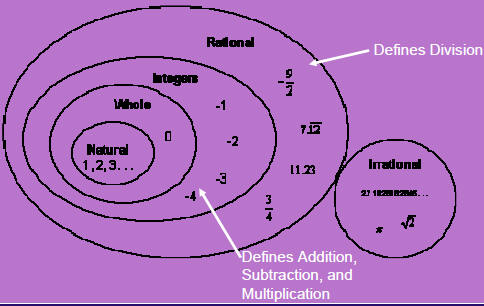
The Real Numbers
| 2 = 2 + 5 Commutative Property of Addition |
 |
5 + t = t + 5 Commutative Property of Addition |
| 3 X 7 = 7 X 3 Commutative Property of Multiplication |
 |
3 X t = t X 3 Commutative Property of Multiplication |
| 3 X 7 X 2 = 7 X 2 X 3 Associative Property of Multiplication |
 |
5 X 3 X t = t X 3 X 5 Associative Property of Multiplication |
| 3 + 5 + 2 = 5 + 2 + 3 Associative Property of Addition |
 |
3 + 5 + t = 5 + t + 3 Associative Property of Addition |
| 3 X (5 + 2) = 3 X 5 + 3 X 2 Distributive Property of Multiplication |
 |
3 X (5 + t) = 3 X 5 + 3 X t Distributive Property of Multiplication |
|
|
||
Key Definitions: Expressions
with More than One Variable
1. Solution of an equation: A value (or an ordered pair of values)
that satisfies the equation
2. Equivalent equations: Equations that have the same solution
set
3. Linear equation: An equation equivalent to one of the form ax
+ by = c with a2 + b2 not equal to 0
4. Function: A rule connecting two sets that assigns to each
element of one set (or input) one and only one element of the
second set (or output)
5. Graph of an equation in two variables: Points in the plane
whose coordinates satisfy the equation
6. Sequence: A function from the positive integers to the real
numbers.
Expressions involving Two or
More Variables…
• Adhere to the same commutative,
associative, and distributive properties:
x(4x3 + 2y3) = x . 4 . x3
+ x . 2 . y3
= 4 . x . x3 + 2 . x . y3
= 4x4 + 2xy3
A Historical Statement on
Translating Word Problems
• In solving a word problem by setting up
equations, the student translates a real
situation into mathematical terms: he has an
opportunity to experience that mathematical
concepts may be related to realities, but such
relations must be carefully worked out. Here is
the first opportunity afforded by the curriculum
for this basic experience.
Process for Translating Word
Problems to Algebra Problems
1. Students verbally read and explain what an
expression/equation means,
2. Students formulate a verbal instruction as an
algebraic expression,
3. Students translate components of word problems
into mathematical expressions,
4. Students construct word problems associated with a
particular algebraic expression
5. Students define variables, and
6. Students explicitly solve problems
Introduction to Functions

Functions Can Be Introduced
Early without Formal Definitions
| Definition A rule between two sets such that there is a unique element in the second set assigned to each in the first set |
Synonyms rule of correspondence
|
|
| function | ||
| f(x) = x + 4 {(1, 2), (3, 2), (5, 1)} Examples |
3y + 5x {(1, 2), (1, 3), (4, 0)} Counter Examples |