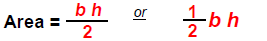Real Numbers
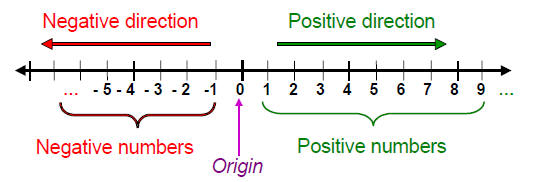
REAL NUMBER LINE:
Draw a straight line and mark a convenient point as zero,
0, then mark equally
spaced distances. Label these as integers → positive to the right and negative
to
the left. To indicate that there are more positive integers to the left and to
the right
we use the symbol “…” which is understood to mean “ and so on” in the pattern
set.
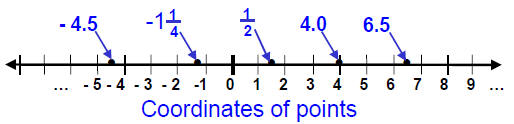
Numbers associated with points on the real number line are
called coordinates of
the points.
Real numbers include whole numbers, fractions, decimals,
and other numbers that
we will see in Section 1.8.
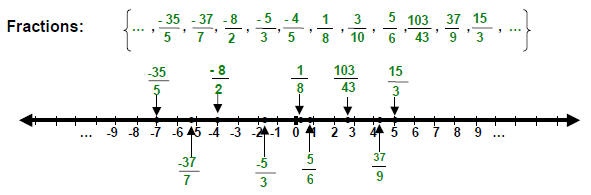
If a and b are real numbers then the expression a/b
is called a fraction. The top number a is called the
numerator and the bottom number b is
called the denominator. Division by zero is not allowed, so b ≠ 0 or the result
is undefined.
Equivalent Fractions: If the numerator and denominator are
multiplied by a common factor ,n,
the resulting expression is an equivalent fraction that has the same numerical
value.
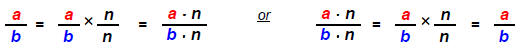
If the numerator and denominator contain a common factor
the expression can be reduced to an
equivalent fraction that has the same numerical value. Answers containing
fraction expressions
must always be left in the “simplest form”.
Equivalent Fractions
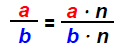
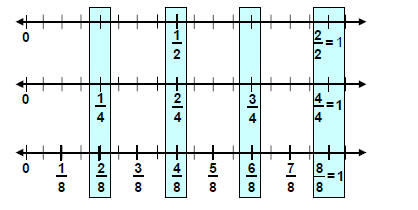
-> Fractions can also be written as decimals if they are
terminating or repeating.
In algebra we write fractions with a larger numerator than denominator in
improper form.
Examples:
Terminating:

Repeating

-> Fractions are sometimes integers when reduced to simplest form:
Examples :
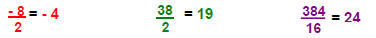
SPECIAL TERMS:
| English words | Math symbols . |
| ABSOLUTE VALUE unsigned number |  |
| OPPOSITES equal value, opposite sign | 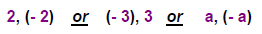 |
| RECIPROCALS numbers with product of 1 | 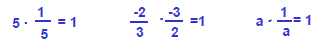 |
ABSOLUTE VALUE: Examples:
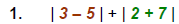 |
Perform inner operations first. |
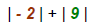 |
Do not drop absolute value symbols here |
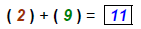 |
Replace absolute values with unsigned numbers and perform resulting operation. |
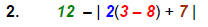 |
Perform inner operations first. |
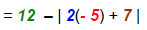 |
Do not drop absolute value symbols here. |
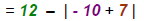 |
Do not drop absolute value symbols here. |
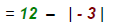 |
Do not drop absolute value symbols here. |
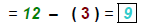 |
Replace absolute values with unsigned number and perform resulting operation. |
CAUTION: Do not “drop” the absolute value “bars”
without performing all operations inside and
do not “drop” them without replacing the resulting number with an unsigned
number.
Equivalent Fractions:
If the numerator and denominator contain a common factor
the expression can be
reduced to an equivalent fraction that has the same numerical value. Answers
containing fraction expressions must always be left in the “simplest form”.
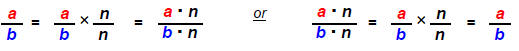
Multiply fractions: Multiply numerators times
numerators and denominators times
denominators.
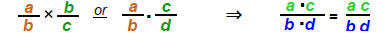
Check the result to see if it will reduce to
[If numerators have common factors with denominators,
factor them out and reduce
before you multiply.]
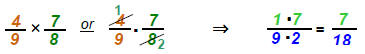
Example: Multiply fractions.
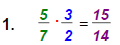
Leave answer as improper fraction.
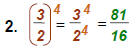
Raise (power) both the numerator and denominator.
Geometry:
A Square:
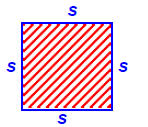
Perimeter = 4 s
Area = s^2
A Rectangle:
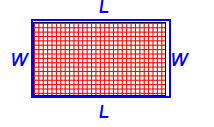
Perimeter = 2L + 2W
Area = L W
A Triangle
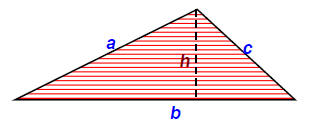
Perimeter = a + b + c