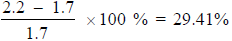Section 8.1 - Percents
• Definition: Percents represent numbers as part of
100
• Converting Fractions to Decimals to Percent:
1. Divide the fraction, it is now a decimal.
2. Move decimal point two places to the right (multiply by 100)
3. Tack a % sign onto the end
Example (Checkpoint 1): 1/8 = 0.125 = 12.5%
Example (Checkpoint 2): 0.023 = 2.3%
• Converting Percent to Decimals
1. Move the decimal point two places to the left (divide by 100)
2. Remove away the percent sign
Example (Checkpoint 3a): 67% = 0.67
•Percentages are used frequently in Application Exercises
Example (Checkpoint 4): In England, the average price per gallon of premium gas
is $4.30. Of
this amount, $3.44 is for taxes. What percent of fuel cost is for taxes?
Solution: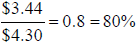
• Recall that “of” in math is multiplication. To find percent “of” a
number, change the percent to a
decimal and multiply
Example (Checkpoint 6): Each year 8000 Americans suffer spinal cord injuries.
13% of these are
due to sports injuries. How many spinal cord injuries are due to sports injuries
each year?
Solution: 13% of 8000 = 0.13 (8000) = 1040 injuries due to sports
•Definition: Sales Tax is a tax rate (as a percentage) times purchase
price
Example (Checkpoint 7): What is the total price of an item for $1260 if the
sales tax is 6%?
Solution:
price + tax = 1260 + 6% of 1260 = 1260 + 0.06 (1260)
= 1260 (1 + 0.06) = 1260 (1.06) = $1335.60
• Definition: Discounts are percentage amounts taken off of the sales
price
Example (Checkpoint 8): A CD player is originally $380, with 35% off. Find the
purchase price
Solution: original price – discount = 380 – 0.35 (380) = 380 (1 – 0.35) = $247
•Definition: Percent increase/decrease is used to
compare changes
It is found with the formula: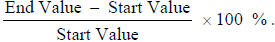
A positive result indicates an increase, and a negative result indicates a
decrease.
Example (Checkpoint 9): Sales went from 1.7 billion in 1998 to 2.2 billion in
1999. What is the
percent increase?
Solution: