Math 150 Lecture Notes for Chapter 2 Equations and Inequalities

Math 150 Lecture Notes for Section 2A Solving Equations

Introduction and Review of Linear Equations

Solve the equation 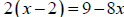  for x. Check your answer.

Solving Quadratic Equations

A quadratic equation is an equation that can be written in the form .

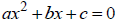I. Solve by Factoring





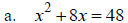
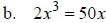
II. Solve by Completing the Square

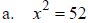
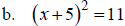
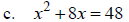
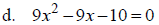
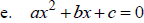
III. Solve by Using the Quadratic Formula
The solution to any quadratic equation of the form is

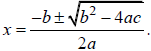
Solve:

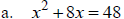
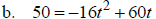
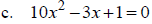
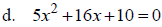
Equations in Quadratic Form
Solve:

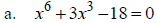
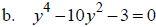
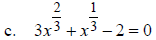
Rational Equations

A rational equation is an equation which involves rational expressions, or fractions.

Solve:

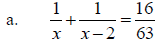
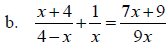
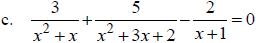
Radical Equations

Strategy to solve radical equations:
1. Isolate one radical.
2. Raise both sides of the equation to the appropriate power to remove the radical.
3. Repeat the process until all radicals have been removed.
4. Check for extraneous solutions!

Solve:

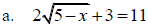
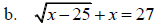
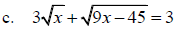
Absolute Value Equation

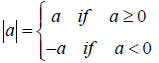
Solve:

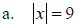
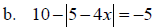
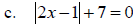
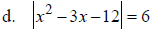
Equations in Several Variables

Solve:

a. Solve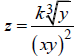for y where

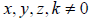
b. Solve 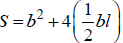for b. Note that S is the surface area of a square right
pyramid where b is the length of a side of the square base and l is the slant height.

Math 150 Lecture Notes for Section 2B Solving Inequalities

Introduction

Find the values of x which satisfies the inequality .

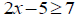Answer as a statement:

Answer as number line graph:

Answer using interval notation:

Linear Inequalities
Note: When you multiply or divide an inequality by a negative number, you must reverse
the inequality sign.

Multiply both sides of 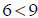by -1.

Solve:

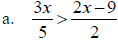
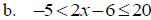
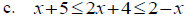
Absolute Value Inequalities

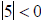  can be thought of as “what numbers are less than 5 units from 0 on the number
line?”

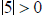can be thought of as “what numbers are more than 5 units from 0 on the number
line?”

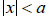is equivalent to

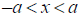
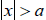is equivalent to

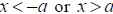
Solve:

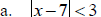
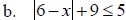
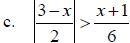
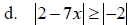
Nonlinear Inequalities

Strategy to solve nonlinear inequalities:
1. Move every term to one side (make one side zero).
2. If possible, factor the expression on the nonzero side.
3. Find the critical values or values for which the expression is zero or undefined.
4. Draw a number line and let the critical numbers divide the number line into
intervals.
5. Determine the sign for each factor in each interval.
6. Determine if the sign for all factors in each interval is positive or negative and
compare to our inequality to see if it is more than or less than zero.

Solve:

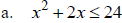
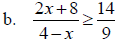(Why don’t we just multiple both sides by 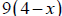to clear all
denominators?)

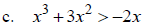  (Why don’t we just divide both sides by x?)