More Math Practice Problems

1 Introduction

The way to learn how to solve problems is to practice. Here are a few problems, including
the entire February 2003 contest!

2 The Algorithm

Some things in life change, but not good contest strategy. First, and most importantly, read
the problem. Make sure you understand it thoroughly, and note the limits. As you think
about an algorithm, think about three things: run time, memory usage, and coding time.
There is a working solution; if your solution doesn’t quite work in time, keep looking! While
an incorrect solution may get significant partial credit, you really rack up points when you
get a full solution, since those last three cases might be worth a third or half of the problem.

3 The Problems

1. (Dwarve’s Casino, UMD 2004 (sort of)) Farmer John wants to gamble with the cows.
But since the cows don’t have opposable thumbs, they can’t do much. So they agreed
that Farmer John will bet some integer amount of money, and the cows will tell him if
he wins or loses. However, out of the N rounds played 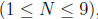the cows can only
make FJ lose L times 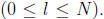Help FJ maximize his winnings given his initial
amount of money D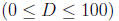

2. (Prisoner, USACO sometime) Bessie has been a bad cow, and FJ wants to put her in
as secure a prison as possible. A prison consists of a set of concentric nonintersecting
closed loops of fences around Bessie, and its security is defined by the number of fences
enclosing her. However, FJ only has a fixed set of N 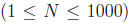posts that he
can build fences between. Given Bessie’s position and these posts, find the maximum
security prison FJ can build around Bessie.

3. (Cow Math USACO Feb 2003)
Taking their cue from the builders of the USA’s Interstate Highway system, the cows
have introduced the Interpasture Path numbering system. They have already numbered
the N (2 ¡= N ¡= 25) pastures with the integers 1..N and now are numbering
each path between two pastures with its own distinct Interpasture Path number in the
range 1..2000 (e.g., I-9 and I-16).

In an example Interpasture Path map, four pastures numbered 1, 2, 3, and 4 are
connected by Interpasture Paths I-3, I-6, I-9, and I-16:

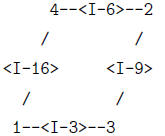
Bessie likes to walk from pasture 1 to pasture 2 on the nifty new Interpasture system.
During each walk, she never visits the same pasture twice, so possible walks on the
sample map above are 1-4-2 and 1-3-2.

Over the years, Bessie has developed an amazing mathematical skill that she likes to
exercise. During each walk, she enjoys finding the greatest common factor (GCF) of the
Interpasture Paths that she traverses. For instance, the walk designated 1-4-2 touches
I-16 and I-6 which have the greatest common factor of 2 (since 2 properly divides into
16 and 6 but no larger integer does).

As she walks the pastures day after day, she takes all the possible routes from pasture
1 to pasture 2 and remembers each of the GCFs. After she has taken every possible
walk once, she computes the least common multiple (LCM) of all the GCFs. For this
example, the two GCF values are 2 and 3 (GCF(6,16)=2 and GCF(3,9)=3), so the
LCM is 6.

For large networks of paths, Bessie might get tired of all the walking, but she really
wants to know the LCM for every map. Calculate that number for her.

4. (Cow Imposters, USACO Feb 2003)
FJ no longer uses the barbaric custom of branding to mark the cows that he owns.
Instead, he creates a binary code of B (1 ¡= B ¡= 16) bits for each cow and embosses
it onto a metal strip that is fastened to each cow’s ear.

The cows have taken in a stray and wish to create an ID strip for it. Unknown to FJ,
they have created a machine that can make a new ID strip by combining two existing
ID strips using the XOR operation (ID strips are not consumed by this machine, and
the same ID strip can be used for both inputs).

The cows wish to create a specific ID strip for the stray or at least get as close to a
desired ID as possible – with the smallest possible number of bits differing between the
goal ID strip and the best possible new ID strip.

Given a set of E (1 ¡= E ¡= 100) existing ID strips, the goal ID strip, and a large
number of blank ID strips to hold intermediate results, calculate the closest possible
ID strip that can be created from the existing ID strips.

If more than one ID is closest, choose the one that can be created in the fewest steps.
If there is still a tie, choose the ‘smallest’ ID (i.e., if you sorted all the IDs, the one
that is first).

5. (Traffic Lights, USACO Feb 2003)
The cows are going downtown! Just like everyone else, they want to optimize their
driving time.

They have noted that when driving on a straight road with traffic lights, the best
strategy to get to their destination as quickly as possible is not necessarily to drive
as fast as possible to the next traffic light, brake if it’s red, wait for a green light,
accelerate, and then drive on. It is often better to approach a traffic light more slowly
in order to have some speed when the light turns green.

The cows have observed the traffic lights for a very long time. They know that each
traffic light behaves in the following way: * it is green for a certain amount of time Tg,
* then it is red for an amount of time Tr, * then green again, * and so on.

Given * the integer length of the road L (1 ¡= L ¡= 100) * the number of traffic lights
N (0 ¡= N ¡= L+1) along with information about each light: * the unique position (0
¡= position ¡= L) * Tg (1 ¡= Tg ¡= 10) * Tr (1 ¡= Tr ¡= 10) * color at t=0 (R or G)
* Tc (the integer amount of time since the light last changed)

write a program to determine the minimal amount of time needed to get to the end of
the road. Note that at each discrete time (starting at t=0), a car may either change
its speed (expressed in positional units per time unit) by one or keep it constant. The
speed is always 0 or positive, of course. No driving backwards!

The car starts at position zero has has speed zero. The car must complete its trip at
position L, also with speed zero. The car must stop at all lights that are red when
encountered – be sure its speed is 0 at the red light’s position if it encounters a red
light. The car may move when the light changes from red to green, but not when it
changes from green to red.

6. (Farm Tour, USACO Feb 2003)
When FJ’s friends visit him on the farm, he likes to show them around. His farm
comprises N (1 ¡= N ¡= 1000) fields numbered 1..N, the first of which contains his
house and the Nth of which contains the big barn. A total M (1 ¡= M ¡= 10000) paths
that connect the fields in various ways. Each path connects two different fields and
has a nonzero length smaller than 35,000.

To show off his farm in the best way, he walks a tour that starts at his house, potentially
travels through some fields, and ends at the barn. Later, he returns (potentially
through some fields) back to his house again.

He wants his tour to be as short as possible, however he doesn’t want to walk on any
given path more than once. Calculate the shortest tour possible. FJ is sure that some
tour exists for any given farm.