Division of Mathematics
Show all work clearly and in order, and box your final
answers. Justify your answers
algebraically whenever possible. You have at most 80 minutes to take this 100
point exam. No
cellular phones allowed. The exam questions are 100 points. Don't forget to sign
your exam!
1. Given
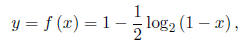
answer each of the following questions.
(a) Rewrite this logarithmic equation in exponential form. That is, solve for x.
Work:
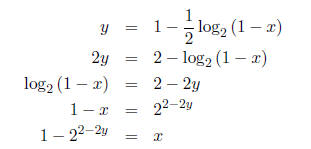
So, we finally have
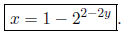
(b) Create a simple table, or list, of at least five ordered pairs (x, y) that are solutions to
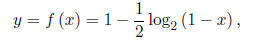
Work: Using 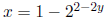 and
using easy values for y, I get:
and
using easy values for y, I get:
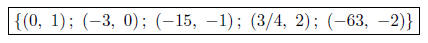
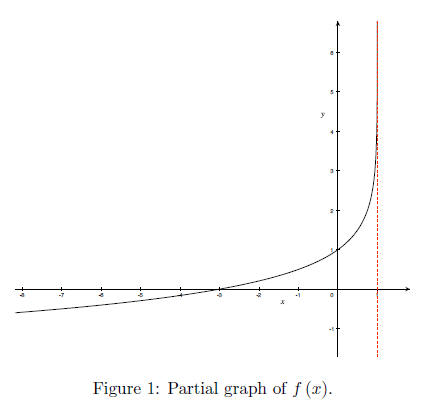
(c) Graph f (x) and be sure to clearly indicate at least one point and all asymptotes.
Work:
2. Given
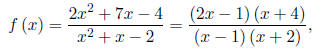
answer each of the following questions.
(a) What is the y-intercept?
Work: Set x = 0, and evaluate to find y. (0, 2)
(b) What are the x-intercepts?
Work: Set y = 0, and evaluate to find x. (-4, 0) and (1/2, 0)
(c) What is the equation of the horizontal asymptote?
Work: This is found by taking a look at two limits, one where
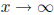 and the other
and the other
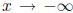 . If you do this you will see that both
limits equal 2. So the horizontal
. If you do this you will see that both
limits equal 2. So the horizontal
asymptote is y = 2 .
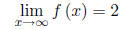
and
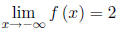
(d) What are the equations of the two vertical asymptotes?
Work: Four limits required.
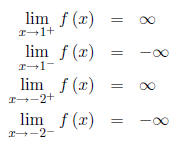
So the vertical asymptotes are: x = 1 and x = -2 .
(e) What is the domain of f (x)?
Work: 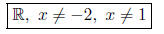
(f) Graph f (x) and be sure to clearly indicate at least one point and all asymptotes.
Work:
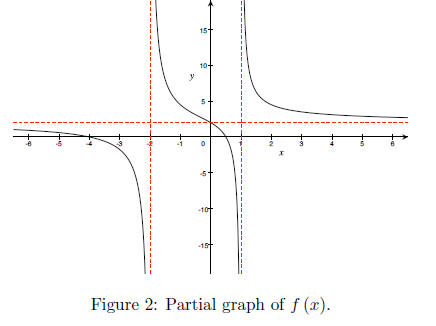
(g) What is the range of f (x)?
Work: R
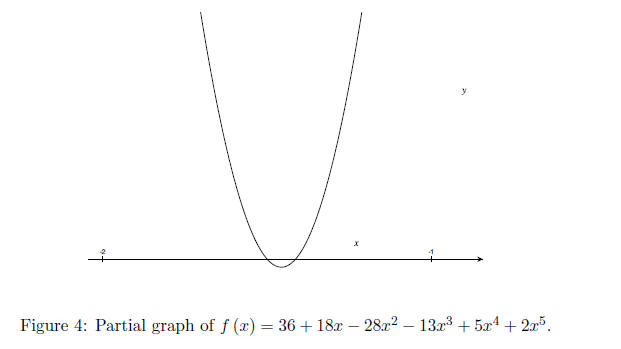
3. Given
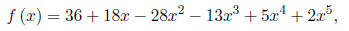
and its graph. Answer each of the following questions.
(a) What is the y-intercept?
Work: Just set x = 0 and you'll get (0, 36) .
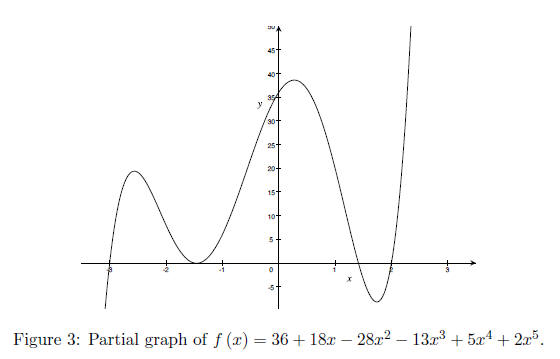
(b) Using the Rational Root Theorem, what are the candidate rational roots?
Work: Writing the ratios out.
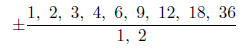
Then you'll need to figure out the set.
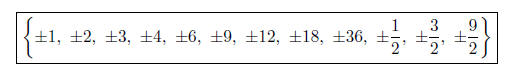
(c) Using the graph, and your answers from (b), what are
reasonable candidates for
rational roots. Test them to see if they actually are.
Work: You should be able to roughly determine the
values of the candidate rational
roots by looking at the graph, and -3, 2, -3/2 and 3/2 are good
candidates if
they're rational. Testing them shows that only three of these are.
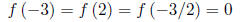
(d) Using (c), factor f (x) completely.
Work: Now we know that x+3, 2x+3, x-2 are factors
of f. Just use long division
to find the missing quadratic factor.
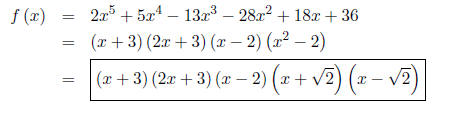
(e) List all roots, real and imaginary.
Work: From above.
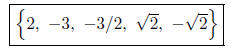
Here's a close-up of the region between -2 and -1. You
should notice the two roots, what
are they? You should also look back at the original graph on page one.