Math 201-1 Final Review Sheet

The final exam covers chapters 1 through 4. No graphing/symbolic calculators allowed and
no notes are allowed. You may bring a simple scientific calculator. You may also bring a 5
inch by 7 inch note card with anything on it. Please no microscopes. The test Monday
December 11th at 1pm until 3pm. Don't be late. Bring photo ID.

Chapter 1: Linear Equations and Functions

§1.1: Solutions of Linear Equations and Inequalities in One Variable: Be able
to solve linear equations, fractional equations, and linear inequalities of one variable. Be
able to solve any linear inequality. For what case does the inequality change direction? Be
able to state the answer using either and inequality, interval notation, or a number line.

§1.2: Functions: Know what a function is. Know when two functions are the same. Be
able to find both the domain and range of a function. Be able to evaluate a function at a
given number, a variable, a smile face, a tree, or an expression. Be able to find and simplify
the difference quotient. Be able to find various combinations of functions, including f(g(x))
and g(f(x)). How does the domain and range of f(x) and g(x) relate to those of f(g(x))?

§1.3: Linear Functions: Know what this is. Be able to find intercepts, both x and y.
What is the difference between slope and rate of change? What is the slope of a vertical
line? What is 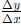? Be familiar with both point-slope and slope-intercept forms of a line. Be
able to construct lines.

§1.5: Solutions of Systems of Linear Equations: Be able to solve a system of
equations using both elimination and substitution where there are two or three variables.
For systems of two variables, what kind of solutions can we have? For systems of three
variables, what kind of solutions can we have?

§1.6: Applications of Functions in Business and Economics: Know the definitions
of fixed cost, variable cost, total cost, total revenue, and profit and how they relate to each
other. What is price times quantity? What is negative profit? What happens when total
revenue equals total cost? Be familiar with both supply and demand functions. Be able to
find market equilibrium. What happens if we add a tax?

Chapter 2: Quadratic and Other Special Functions

§2.1: Quadratic Equations: Be able to solve a quadratic equation. Be able to factor.
Memorize the quadratic formula. What are valid answers? Be able to solve problems that
are equivalent to quadratic equations. For example

and

§2.2: Quadratic Functions: Parabolas: Know what these are. Be familiar with
intercepts, the vertex, axis of symmetry, and concavity. Be able to find average rate of
change. Be able to find the slope of a secant line. Be able to maximize profit and revenue.
Be able to minimize cost.

§2.3: Business Applications of Quadratic Functions: Be able to find market equi-
librium. Be able to find break-even points. Be able to maximize money.

§2.4: Special Functions and Their Graphs: What is a constant function? What is
the identity function? What are power functions? What are polynomial functions? What
are root functions? What are rational functions? Be able to find the asymptotes of rational
functions. What is a piecewise function?

Chapter 3: Matrices

§3.1: Matrices: Be able to state the size (dimension of a matrix). Know what row and
column (matrices) vectors are. Be able to construct a matrix given a formula. Be able to
solve a matrix equation. Know what a diagonal matrix, a upper triangular matrix, and a
lower triangular matrix are. Be able to perform matrix addition and scalar multiplication.
Know what the transpose of a matrix is. What is the zero matrix? What is the transpose
of a matrix? Be able to set up a matrix to represent real world data.

§3.2: Multiplication of Matrices: Know when we can multiply two matrices together.
Be able to multiply two matrices together. What is the transpose of a matrix product? What
is the identity matrix and what properties does it have? What is the power of a matrix? Be
ready for a real world application regarding this. Is there such a thing as matrix division?

§3.3: Gauss-Jordan Elimination: Solving Systems of Equations: Know the dif-
ference between an augmented matrix and a coefficient matrix. Be able to state the three
elementary row operations. Be able to use the three row operations to reduce a matrix.
Know what a reduced matrix. Know what the leading coefficients are and how they are
positioned in a reduced matrix. Be able to solve a linear system by using matrix reduction
(Gauss-Jordan Elimination). If a leading coefficient is in the right most column of an aug-
mented matrix, how many solutions are there? If not every column of the coefficient matrix
has a leading coefficient, how many solutions are there?

§3.4: Inverse of a Square Matrix; Matrix Equations: Know when an inverse of a
matrix exists? Is it unique? Be able to find the inverse of a matrix if it exists. Be able to
solve a linear system by using the inverse of the coefficient matrix. Ax = b => x = A^-1b.
Be able to find the determinant of a matrix. What does the determinant tell us?

Chapter 4: Inequalities and Linear Programming

§4.1: Linear Inequalities in Two Variables: Be able to graph of solution set of a
system of inequalities in two variables. Be able to find the vertices of this solutions sets. Be
able to express a real world situation using a system of inequalities.

§4.2: Linear Programming: Graphical Methods: What is a linear program? Be
able to solve a given linear program graphically. What is a feasible region? Note that we
can either maximize or minimize. Be able to solve a real world program. When will we have
multiple solutions?

§4.3: The Simplex Method: Maximization: What is the Simplex method? Know
how to implement it to solve a maximization linear program. Be able to use it to solve a
real world problem. Graphically, what is going on with the vertices?

§4.4: The Simplex Method: Duality and Minimization: Given a standard min-
imization problem, be able to solve it by instead solving its dual problem. Note that the
original problem is called the primal problem. Be able to use it to solve a real world problem.

§4.5: The Simplex Method with Mixed Constraints: Given any maximization or
minimization problem in nonstandard form, by able to convert it to a standard maximization
problem. What condition must all of the constraints be in for a standard maximization
problem? If we have any right-hand side of any constraint with a negative number, how do
we choose the pivot? Graphically, what is going on? Be able to use it to solve a real world
problem.

Chapter 5: Exponential and Logarithmic Functions

§5.1: Exponential Functions: Know the definition of a basic exponential function. What
is its domain and range? Be familiar with its graph. Does it have any asymptotes? Be
able to graph an exponential if it has been shifted, reflected, or stretched. What is the
normal distribution? Continuous interest and depreciation are examples of the importance
of exponential functions. What is the most important base?

§5.2: Logarithmic Functions and Their Properties: What does it mean for a function to
be one-to-one? What condition must be satisfied in order for a function to be invertible?
What is the inverse of an exponential function? Graphically, two functions that are inverses
of each other are reflected across the identity function f(x) = x. What are the two important
bases? Market share and the Richter scale are examples where logs are used. Know all of
the properties of logarithms: products, ratios, powers, inverses, and change of base. Be able
to both expand and compact expressions with log terms.

§5.3: Solutions of Exponential Equations: Applications of Exponential and Logarithmic
Equations: Be able to solve exponential equations.

Look over this list and the sample exams. I could give an application problem that would
cover any or all of the above. I will have office hours on Monday from 10:30 until 12:30.