Try the Free Math Solver or Scroll down to Tutorials!

Enter expression, e.g. (x^2-y^2)/(x-y)

Enter expression, e.g. x^2+5x+6

Enter expression, e.g. (x+1)^3

Enter a set of expressions, e.g. ab^2,a^2b

Enter equation to solve, e.g. 2x+3=4

Enter equation to graph, e.g. y=3x^2-1

Depdendent Variable

Number of equations to solve:

Equ. #1:

Equ. #2:

Equ. #3:

Equ. #4:

Equ. #5:

Equ. #6:

Equ. #7:

Equ. #8:

Equ. #9:

Solve for:

Enter inequality to solve, e.g. 2x+3>4

Enter inequality to graph, e.g. y<3x^2-1

Dependent Variable

Number of inequalities to solve:

Ineq. #1:

Ineq. #2:

Ineq. #3:

Ineq. #4:

Ineq. #5:

Ineq. #6:

Ineq. #7:

Ineq. #8:

Ineq. #9:

Solve for:

Math solver on your site

Please use this form if you would like
to have this math solver on your website,
free of charge.

Name:

Email:

Your Website:

Msg:

Radian,Arc Length,and Area of a Sector

An angle is formed by two rays that share a common endpoint called the vertex of the angle. The vertex can
represent a point of rotation in that one ray is the initial side of the angle before rotation and the other ray
forms the terminal side after the rotation.

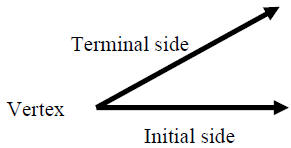
One principal means of measuring the size of an angle is using degree measure. An angle formed by the
rotation of a ray through one complete circle measures 360 degrees.

Another principal means of measuring the size of an angle is using radian measure. Begin with a circle of
radius r and let θ be a central angle, an angle whose vertex is the center of the circle. Let s be the
length of the arc that is intercepted by the angle. The radian measure of θ is given by θ = s/r,
where r and s have the same linear units.

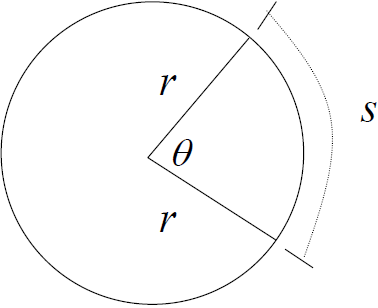
Example 1: A circle has a radius of 9 inches. A central angle, θ, intercepts an arc of length 36
inches. What is the radian measure of θ ?

Example 2: A circle has a radius of 24 inches. A central angle, θ, intercepts an arc of length 7
feet. What is the radian measure of θ?

To devise a formula for converting between degree measure and radian measure consider the right angle
shown in the figure below.

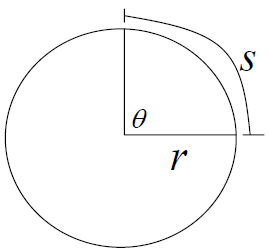
Since θ measures 90° the arc length s is 1/4 the circumference of the circle.

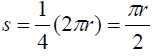
Use the formula for radian measure and substitute 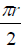for s.

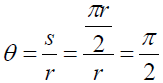
Therefore,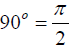 radians.

To obtain formulas for converting between degree measure and radian measure, multiply
both sides of the equation above by 2 180° = π radians.

From the formula above, we see that 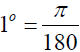rasians ( ≈ 0.017 rasian ) and 1radian = 180/π (≈ 57.3°).

To convert from degree measure to radian measure, multiply degrees by π/180°.

To convert from radian measure to degree measure, multiply radians by 180°/π.

Common Angles

Memorize the common angles.

Example 3: If two angles of a triangle have radian measures 2π/7 and π/9, find the radian measure of
the third angle.

Example 4: Convert the following degree measure to radians.
300°

Example 5: Convert the following degree measure to radians.
50°

Example 6: Convert the following radian measure to degrees.
7π/4

Example 7: Convert the following radian measure to degrees.
π/12

In a circle of radius r, the arc length s that is determined by a central angle of radian measure θ is given by the
arc length formula s = rθ. where r and s have the same linear units.

In a circle of radius r, the area A of a sector with central angle of radian measure θ is given by the
area sector formula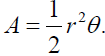

Example 8: Find the radius of a circle if the length of the intercepted arc by a central angle 4π/3
is 39π/2 inches.

Example 9: Find the sector area determined by a circle that has a radius of 5 cm and central angle 7π/6.

Example 10: A sector of a circle has a central angle 135° and area 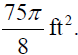Find the radius of the
circle.

Your Math Help is on the Way!

More Math Help

Radian,Arc Length,and Area of a Sector