INTERMEDIATE ALGEBRA
I. SETS
A. Define set, element, finite and infinite sets, empty set
B. Relations between sets: subset, proper subset, equal sets
C. Set operations: union, intersection and complement
D. Set-builder notation
E. The set of natural numbers
F. The set of integers
G. The set of rational numbers
H. The set of real numbers
1. Operations
2. Commutative, associative, and distributive properties
3. Identity and inverse elements
II. LINEAR EQUATIONS AND INEQUALITIES IN ONE VARIABLE
A. Review of techniques for solving linear equations and inequalities in one
variable
B. Review solving literal equations for a specified variable
C. Absolute value
1. Definition and examples
2. Equations of the form |*ax + b*|= c
3. Inequalities of the form |*ax + b *|< c
4. Inequalities of the form |*ax + b *|> c
D. Word problems (mixture, distance, age, money, and interest)
III. LINEAR EQUATIONS AND INEQUALITIES IN TWO AND THREE VARIABLES
A. Definition and examples of linear equations
B. Review of the rectangular coordinate system
C. Graphing linear equations in two variables
1. Intercept method
2. The slope concept
3. The slope-intercept form
D. Systems of linear equations in two variables
1. Classification of systems: Consistent, inconsistent, and dependent
2. Representation by graphs
3. Substitution
4. Elimination by addition
E. Systems of linear equations in three variables
1. Classification: unique solution, no solution, infinite number of
solutions
2. Substitution
3. Elimination by addition
F. Solving graphically linear inequalities in two variables
G. Solving graphically systems of linear inequalities in two variables
IV. POLYNOMIALS IN ONE OR MORE VARIABLES
A. Laws of integral exponents; multiplication of
monomials
B. Addition and subtraction
C. Multiplication of two polynomials, including FOIL method
D. Special products
1. Square of a binomial
2. Multiplying the sum and difference of two terms
E. Division
1. Polynomial by a monomial
2. Polynomial by a polynomial
F. Factoring
1. Polynomials with a common factor
2. The difference of two squares
3. Perfect square trinomials
4. General trinomials
5. Sum and difference of perfect cubes
6. Factoring by grouping
V. ALGEBRAIC FRACTIONS
A. Multiplication and division
B. Simplest form of a fraction, restrictions on the variable
C. Least common multiple
D. Addition and subtraction
E. Complex fractions
F. Fractional equations that reduce to linear equations
VI. EXPONENTS AND RADICALS
A. Radicals
1. Definitions
2. Laws of radicals
3. Simplest radical form
B. Operations with radical expressions
1. Addition and subtraction
2. Multiplication
3. Division: rationalizing denominator
(including conjugates and roots other than the square root)
C. Rational exponents
1. Definitions
2. Laws of exponents
3. Simplifying expressions involving rational exponents
D. Solving equations involving radicals that reduce to linear equations
VII. QUADRATIC EQUATIONS
A. Review of solving by factoring
B. Factoring by completing the square
C. Quadratic formula (derivation and use)
D. Word problems
1. Number problems
2. Area problems
E. Graphing parabolas
1. Vertex
2. Intercepts
3. Symmetry
F. Solving quadratic inequalities
G. Solving fractional and radical equations that reduce to quadratic
equations
VIII. RELATIONS AND FUNCTIONS
A. Definition and examples
B. Domain and range
C. Graphs
D. Functions
1. Definition and examples
2. Notation
3. Graphs and the vertical-line test
IX. LOGARITHMS
A. Definition
B. Base ten logarithms and antilogarithms (computation kept to a minimum)
C. Laws of logarithms
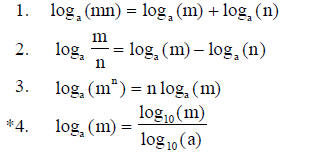
*5. Solving simple exponential and logarithmic equations
*Optional


