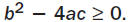Solve Quadratic Equations by the Quadratic Formula
Goals • Solve quadratic equations using the
quadratic
formula.
| Your Notes | VOCABULARY Quadratic formula A formula that gives the solutions of any quadratic equation in standard form |
|
| THE QUADRATIC FORMULA The roots of the polynomial 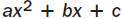 and the
and thesolutions of the quadratic equation
|
||
| Example 1 Multiple Choice Practice | ||
Which is one of the solutions to the
equation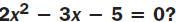  |
||
| Solution | ||
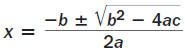 |
Quadratic formula | |
 |
Substitute values in the quadratic formula: a = 2 , b = -3 , and c = -5 . |
|
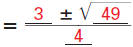 |
Simplify. | |
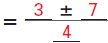 |
Simplify the square root. |
|
One solution is -1. The correct
answer is B |
||
| Your Notes | Example 2 Use the quadratic formula | |
| Crabbing A crabbing net is thrown
from a bridge, which is 35 feet above the water. If the net's initial velocity is 10 feet per second, how long will it take the net to hit the water? Solution The net's initial velocity is v = 10 feet per second and the net's initial height is s = 35 feet. The net will hit the water when the height is 0 feet. |
||
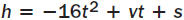 |
Vertical motion model | |
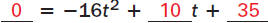 |
Substitute for h, v, and s. | |
 |
Substitute values in the quadratic formula: a = -16 , b= 10 , and c = 35 . |
|
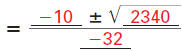 |
Simplify. | |
The solutions are
 and and |
||
| Because time cannot be a negative number, disregard the negative solution. |
 So, the net
will hit the water So, the net
will hit the waterin about 1.82 seconds. |
|
 Guided
Practice Complete the following exercises. Guided
Practice Complete the following exercises. |
||
1. Use the quadratic formula to solve
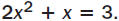 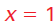 and and
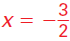 |
||
| 2. In Example 2, suppose the net was
thrown with an initial velocity of 5 feet per second from a height of 20 feet. How long would it take the net to hit the water? about 1.29 seconds |
||
| Your Notes | METHODS FOR SOLVING QUADRATIC EQUATIONS | |
| Methods | When to Use | |
| Factoring | Use when a quadratic equation can be factored easily. |
|
| Graphing | Use when approximate solutions are adequate. |
|
| Finding | Use when solving an equation that can | |
| square roots | be written in the form x2 = d . | |
| Completing | Can be used for any quadratic equation | |
| the square | Can be used for any quadratic equation the square when a = 1 and b is an even number. |
|
| Quadratic | Can be used for any quadratic equation. | |
| formula | ||
| Example 3 Choose a solution method | ||
| Tell what method(s) you would use to
solve the quadratic equation. Explain your choice(s).  Solution a. The quadratic equation cannot be factored easily and completing the square would result in many fractions . So, the equation can be solved using the quadratic formula . b. The quadratic equation can be solved using square roots because the equation can be written in the form x2 = d. |
||
|
|
||
| Homework | 3. Tell what method(s) you would use
to solve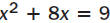 . Explain your choices(s). . Explain your choices(s).factoring: the expression can be factored easily; completing the square: the equation is of the form even number. |
|



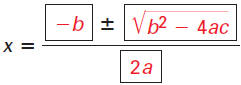 when
when