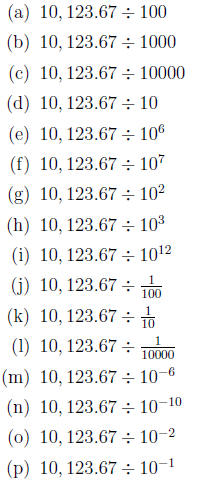Rational Numbers Worksheet
1. Which of the following are true?
(a) The rational numbers are commutative under addition.
(b) The rational numbers are commutative under subtraction.
(c) The rational numbers are commutative under multiplication.
(d) The rational numbers are commutative under division.
(e) The rational numbers are associative under addition.
(f) The rational numbers are associative under subtraction.
(g) The rational numbers are associative under multiplication.
(h) The rational numbers are associative under division.
(i) The rational numbers are closed under addition.
(j) The rational numbers are closed under subtraction.
(k) The rational numbers are closed under multiplication.
(l) The rational numbers are closed under division.
(m) Every rational number has an additive inverse.
(n) Every rational number has an multiplicative inverse.
(o) Every rational number has a unique additive inverse.
(p) Every nonzero rational number has a unique multiplicative inverse.
(q) One is the multiplicative identity for the set of rational numbers.
(r) Zero is the additive identity for the set of rational numbers.
(s) If 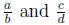 are distinct rational numbers with
are distinct rational numbers with
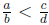 , then there is a rational number
, then there is a rational number
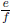 such that a
such that a
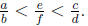
(t) (problem 21 from section 6.1) There are infinitely many rational numbers
between 0 and 1.
(u) (problem 21 from section 6.1) There are infinitely many ways to replace two
fractions
with two equivalent fractions that have a common denominator.
(v) (problem 21 from section 6.1) There is a unique least common denominator for
a given
pair of fractions.
(w) (problem 21 from section 6.1) There is a least common fraction.
2. Find the additive inverse.
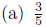
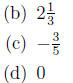
3. Find the multiplicative inverse, if possible.
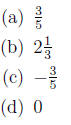
4. Find a rational number that is between the two rational numbers you are given.

5. Explain why we define
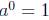 and
and 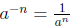 when
a ≠ 0 and n is a positive integer. (See the
when
a ≠ 0 and n is a positive integer. (See the
discussion on pages 415{416.)
6. Write each decimals in expanded form.
(a) 456.6787
(b) 0.7856
(c) 123.6712143
7. Quickly multiply.

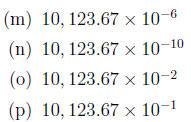
8. Quickly multiply.