Math 1010-3 Exam #3 Review Guide

*This is only a guide, for your benefit, and it in no way replaces class notes, homework, or studying*

General Tips for Studying:
1. Review this guide, class notes, the text, and rework examples done in class
2. Review comments on quizzes and rework ALL quiz problems
3. Review (assuming you have already completed it) ALL homework assigned for 6.69.2
4. Complete ALL suggested problems for the exam review given in class
5. Start studying early enough to ask questions!

Chapter 6: Rational Expressions, Equations, and Functions
6.6 Solving Rational Equations (This WILL be on the Exam):
• Be able to solve rational equations with constant or variable denominators
• Remember! The first step is to multiply each term by the LCD of ALL fractions involved
(NOT the LCD/LCD)
We are not trying to get a common denominator, we are trying to eliminate all
denominators (so the resulting equation is either linear or quadratic)
• Remember! You MUST check for extraneous solutions. In these problems, that means we
must check if our answer(s) give a zero denominator in the ORIGINAL equation. If an
answer does, then it is not a solution of the equation.

Chapter 7: Radicals and Complex Numbers
7.1 Radicals and Rational Exponents:
• Know how to evaluate the nth roots of numbers and evaluate radical expressions
Remember! In this book we usually use the principle square root (the nth root
that has the same sign as the radicand)
• Know properties 1 and 2 on page 447 (Because we covered 7.6, we can now take even
roots of negative numbers, so rule 3 no longer applies)
• Know properties 1 and 2 on page 448 (Remember the absolute value if n is even!)
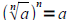a
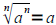If n is odd, then . If n is even, then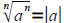
• Understand how to change exponents to radicals and radicals to exponents
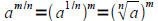AND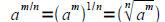
Remember! Either method gives you the same result, but sometimes one is easier
to compute than the other
• Be able to use our previous exponent rules (see table page 449) with rational exponents
• Be able to find the domain of a radical function
If n is odd, the domain of 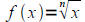is all real numbers
If n is even, the domain of 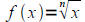is the set of all nonnegative real numbers
(we must still restrict this because we only plug in real numbers)

7.2 Simplifying Radical Expressions:
• Use the product and quotient rules to simplify radical expressions
If the nth roots of u and v are real, then
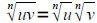AND

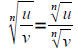
• Be able to rationalize the denominators (to remove any radicals) of radical expressions

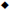7.3 Adding and Subtracting Radical Expressions:

• Be able to combine like radical terms to add or subtract radical expressions

7.4 Multiplying and Dividing Radical Expressions:

• Know how to use the distributive property and FOIL to multiply radical expressions
• Know what conjugates are and be able to use conjugates to rationalize two term
denominators of radical expressions
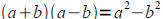The idea here is that so our middle term cancels out

7.5 Radical Equations and Applications (This WILL be on the Exam):

• Be able to solve radical equations

For single radical equations: isolate the radical and then raise each side of the
equation to the appropriate nth power (2 for square roots, 3 for cube roots).
Then, solve the resulting equation.
For multiple radical equations: try to isolate a radical on each side, then follow
the steps as above. If you cannot isolate the radicals then raise each side to the
nth power, but notice that there will be a radical in the resulting equation. You
must then isolate this new radical and do the process again.
• Remember! You MUST check for extraneous solutions. In these types of problems,
extraneous solutions are ones that simply do not solve the ORIGINAL equation. Raising
to the nth power sometimes introduces these extra "solutions."
ALWAYS check the solutions in the original equation, do NOT raise both sides to
the nth power while you are checking!!!

7.6 Complex Numbers:

• Be able to write numbers in i-form
and perform operations with these numbers
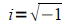so that
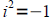
This means that
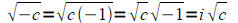
• Know how to add, subtract, and multiply complex numbers
• Understand what complex conjugates are and be able to use them to write the quotient
of two complex numbers in standard form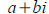
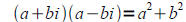(pay special attention the the + sign here)

Chapter 8: Quadratic Equations, Functions, and Inequalities
**Remember! If the directions of a problem ask you to use a certain method, you MUST use that
method or you will receive no credit.**

8.1 Solving Quadratic Equations: Factoring and Special Forms:

• Solve quadratic equations by factoring (already tested on Exam 2)
• Solve quadratic equations by using the Square Root Property (both real and complex)

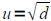If u²=d where d>0 then and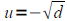
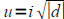If u²=d where d<0 then and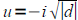

8.2 Completing the Square:

• Rewrite quadratic expressions in completed square form and be able to solve quadratic
equations by completing the square
To complete the square for 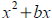add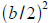
Note that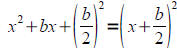
Remember! If the leading coefficient is NOT 1, you must make it one by dividing
the entire equation by that coefficient BEFORE completing the square

8.3 The Quadratic Formula:

• Use the quadratic formula to solve quadratic equations

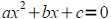The solutions of are given by

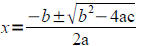
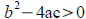Remember! If the equation has 2 real solutions. If b²−4ac=0 the
equation has one repeated real solution. If 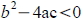the equation has no real
solutions (two complex solutions)

8.4 Graphs of Quadratic Functions (See my handout from class):
• Be able to sketch parabolas, 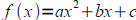, using the following information:
The vertex of a parabola is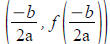 (You can complete the square to find
the vertex, but I suggest memorizing this formula)
The parabola opens up if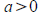 and down if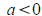
The x intercept(s) (let y=0 and solve for x) and the y intercept (let x=0 and solve
for y...notice this always gives you y=c) (You can just plug in random points, but I
suggest the intercepts...they are easy to find and graph)

Chapter 9:Exponential and Logarithmic Functions

9.1 Exponential Functions:

• Be able to evaluate exponential functions
• Know how to build a table of values to graph exponential functions
• Know how to use transformations and reflections to graph exponential functions
• Note : On the exam you will only be required to simplify as much as possible without a
calculator, you will not be expected to get decimal approximations. Numbers will be
reasonable to work with without a calculator.

9.2 Composite and Inverse Functions:

• Understand function composition: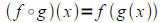
This is read f“ of g of x”
Remember! Function composition is NOT multiplication!
• Note : Finding inverse functions will be covered on Quiz 10 and the Final Exam

Just a Reminder...
You are responsible for knowing and applying all material covered on Exam 1 and Exam 2
as it relates to the current material being tested.