Basic Operations with Decimals: Division

3.2: Basic operations with decimals:
Division

Quick division vocabulary review:

◦ Dividend: the first number in a division
problem; the number being divided.

◦ Divisor: the second number in a division
problem; the number the dividend is
divided into.

◦ Quotient: the answer in a division
problem.

Dividend / Divisor = Quotient

First, we’re going to introduce two
tricks to dividing with decimals points:

◦ Using the long division we’ve already
learned to divide using decimal points.

◦ Shifting the decimal points in division to
make the problem easier

Division with decimals is very similar to
division with whole numbers.

Review: 116/2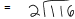

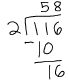
116/2 = 58 and 1.16/2 = 0.58

	We do the long division exactly the same, just line the decimals up.

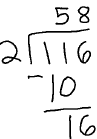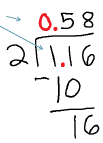We can shift the decimal points in a
division problem to make it easier.

Notice the following:

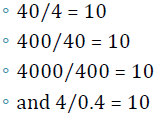	Notice where the decimal point is moving!

As long as we move the decimal point in
the same direction and the same
number of places for both numbers, we
have an equivalent problem.

These all are equal to 10.

All of these expressions are the same.
We’ve only moved the decimal point in each .

So, let’s try an example with the two
things we’ve just learned:

◦ Using the long division we’ve already
learned to divide using decimal points.

◦ Shifting the decimal points in division to
make the problem easier.

Example: 4.56/0.4

◦ (We can get rid of the decimal point in 0.4)

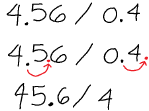
So, now we’re dealing with the problem

45.6 / 4
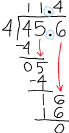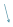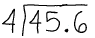Using long division, we arrive at the answer, 45.6/4 = 11.4

Example: 3.5 / 0.02

This problem becomes much
easier when the divisor gets rid
of its decimal!

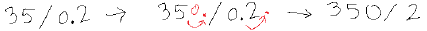
Now, we’ve reduced the problem
into an equivalent problem.

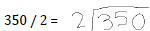
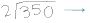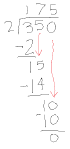As shown in the long division, the answer is 175.

Example: 16.48 / 1.6

◦ First step: Let’s get rid of the decimal place
in the divisor (which is 1.6).

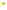Remember: We have to do the same thing to
both numbers!

Now we have this expression.

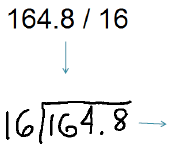	Don’t forget to keep the decimals in line.

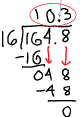RULE: Division of decimal numbers:

◦ Move the decimal point in the divisor to
obtain a whole number.

◦ Move the decimal point the same number of
places in the dividend.

◦ Proceed with division as with whole
numbers.

◦ Line up the decimal point in the long
division with the quotient.

3.2: Basic operations with decimals:
Terminating and nonterminating decimals

Up to this point, in all of our division
problems, the quotient has been a
whole number.

◦ It is not always the case.

You may have learned to use a
“remainder” in division.

◦ Example: 46 / 7 = 6 R4

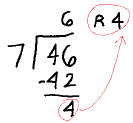
In practical life, we rarely use this
notation.

When the quotient comes out exactly, it is
called a terminating decimal.

◦ Example: 1 / 2 = 0.5
◦ 0.5 is a terminating decimal.

When the quotient does not end, it is
called a nonterminating decimal.

◦ Example: 10 / 3 = 3.333…

◦ 3.333… is a nonterminating decimal.

◦ 3.333… can be written as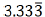

Since the 3 is repeated forever, it is called a repeating decimal.

Example: 46 / 7	If we continued this long division forever, we would never finish. We would eventually see that the digits repeat themselves after a certain point. 46 / 7 = 6.571428571428… Here is another repeating decimal.

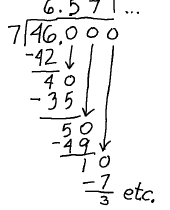3.2: Basic operations with
decimals: Irrational numbers

Some numbers are nonterminating and
nonrepeating.

◦ They go on forever, and the digits never
repeat.

◦ Examples:


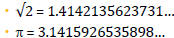
  Both of these numbers neither end, nor repeat.

3.3: Percents: Conversions from
percent to decimal

% is the percent sign.

“Percent” means “per hundred”

So, 100% is 100 per 100.

◦ Or, 100% is the “whole thing.”

“Per” tells us to divide.

◦ To change a percent into a decimal, replace
“%” with “divided by 100”
This would mean to shift the decimal point two
places to the left.

Example: 50%
◦ We replace “%” with “divided by 100”
50%→ 50 divided by 100 → 50 / 100
= 0.5

◦ Does this make sense?
We know 50% is half.
0.5 is half.

Example: 100%
◦ We replace “%” with “divided by 100”
100% →100 divided by 100→ 100 / 100
= 1

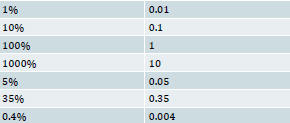
Examples:

Percent	Expressed as a decimal

Let’s prove that our decimal equivalent
of a percent works in real life:

◦ A $10 movie ticket is 50% off.
Replace 50% with 0.5

◦ How much is the ticket?
$10 * 0.5 = $5

◦ We generally work with the decimal
equivalent of a percent in mathematics.

3.3: Percents: Conversions from
decimal to percent

To change any number into a percent,
multiply by 100%.

◦ This would mean shifting the decimal to
places to the right.

Example: Change 0.75 into a percent

◦ Multiply by 100%
0.75 * 100% = 75%

If we ever forget which direction to
move the decimal when converting,
think of it practical terms.

◦ Half?
◦ A half is 50%
◦ A half is also 0.5

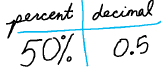
Always think of the simplest example you can come up
with if you can’t remember the rule.

A rule is a rule because it always works!

Homework

Exercise 3.2.4:

◦ 1, 2, 4, 5, 11.

Exercise 3.2.7:

◦ 1, 4, 5, 6.

Exercise 3.3.1:

◦ 1ab, 2a, 3a, 4ab.

Exercise 3.3.2:

◦ 1a, 2ab, 3a, 5a.