Algebraic Symmetries
Symmetries IV
This means that, from an abstract point of view,
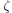 is simply a number
is simply a number
that satisfies the equation
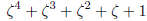
and no other. But  ,
,  and
and 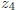 have exactly the same
property. Thus for
have exactly the same
property. Thus for
strictly algebraic purposes we could take
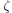 to be
to be 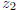 rather than
rather than 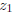 . Thus
. Thus 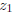 is
is
replaced by 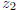 . Since all algebraic relations are to be preserved, this entails
. Since all algebraic relations are to be preserved, this entails
replacing 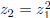 by
by
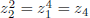 and
and 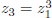 by
by
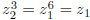 . Once again,
. Once again,
because all algebraic relations are to be respected, the number
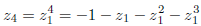
is to be replaced by
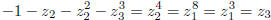
In general a number
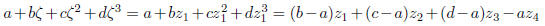
is replaced by
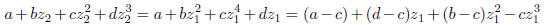
which is a number of the same kind. For example
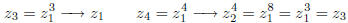
Forms of algebraic symmetries
The symmetry just examined can be viewed in two ways:
1) It takes the sequence 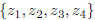 of all roots of
of all roots of
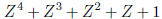
to a sequence formed from the same numbers but in a different order
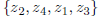
2) It takes any number

to a number

of the same kind.
This is the kind of symmetry that was later investigated in general by
Galois. We have to spend some time growing accustomed to it. Suppose we
apply the symmetry twice. Then
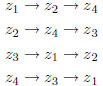
Thus applying the basic symmetry twice leads to the first
symmetry considered,
complex conjugation. We apply it again.
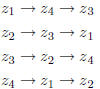
Yet again!
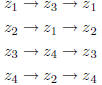
So the symmetry when repeated four times comes back where
it began. It is
a four-fold symmetry.
Anticipating Galois and his successors
No matter which of the numbers 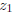 ,
, 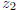 ,
, 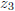 ,
, 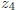 we take
we take
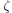 to be, the
to be, the
collection of numbers
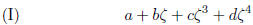 ,a, b, c, d all
fractions
,a, b, c, d all
fractions
is the same. Modern mathematicians usually call the
collection a field. the
sum and the product of two numbers of this sort are again numbers of the
same sort. This we have seen already. I give another example.
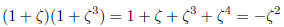
Any symmetry of this collection that respect the algebraic
operations will
take 0 to 0 and 1 to 1. Then adding and dividing it takes any fraction a/b to
a/b. Moreover any root of
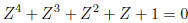
will be taken to another root. Thus 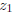 will be taken to
will be taken to
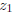 ,
, 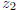 ,
, 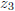 or
or 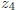 .
.
In other words, the symmetry will be one of the four (including the trivial
symmetry!) we already have. Denote the one taking 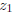 to
to 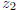 by the letter
by the letter
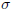 .
.
Then the repeating 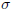 to obtain
to obtain
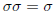 we obtain the symmetry taking
we obtain the symmetry taking 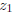 to
to
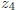 . Repeating again, we obtain
. Repeating again, we obtain
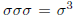 which takes
which takes 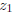 to
to 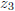 . Repeating
. Repeating
again, we find that 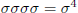 is the trivial symmetry.
is the trivial symmetry.
Inside the collection of numbers there is a smaller collection of numbers
that have a special symmetry. We met them before. They are those that
are not affected by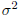 , thus by complex conjugation. They are the numbers
, thus by complex conjugation. They are the numbers
a+ bw, w = 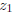 +
+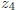 . We were able to construct
. We were able to construct 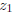 by succesive square roots, by
by succesive square roots, by
first singling out this special collection of numbers, finding that any number
in it satisfied a quadratic equation with fractions as coefficients, in particular
that w2+w−1 = 0, so that 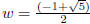 , and then solving
, and then solving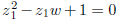 .
.
We now apply these ideas, which I hope are clear, to the heptadecagon!
The Heptadecagon
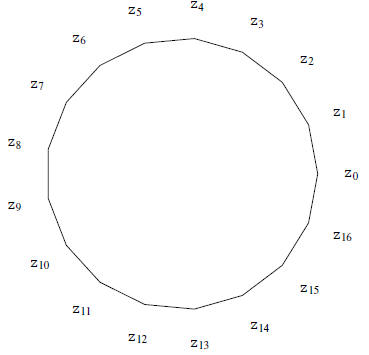
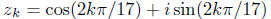
From the Disquisitiones Arithmeticae
There is a famous remark from the introduction to the seventh
and last chapter of the Disquisitiones that I quote here. What it
anticipates is the study of the division points on elliptic curves, in
the remark a special elliptic curve, a study that led over the course
of the nineteenth and twentieth century to many things, especially
complex multiplication and l-adic representations, that are relevant
to the Shimura-Taniyama-Weil conjecture,
Ceterum principia theoriae, quam exponere aggredimur, multo
latius patent, quam hic extenduntur. Namque non solum ad functiones
circulares, sed pari successu ad multas alias functiones transscendentes
applicari possunt, e. g. ad eas, quae ab integrali
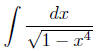
pendent, praetereaque etiam ad variam congruentarium
genera: sed
quoniam de illis functionibus transscendentibus amplum opus peculiare
paramus, de congruentibus autem in continuatione disquisitionum
arithmeticarum copiose tractabitur, hoc loco solas functiones
circulares considerare visum est.
Lecture 7
A proof by Gauss (beginning)
Recall that we want to show that 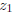 is a root of the equation
is a root of the equation
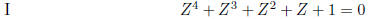
but of no equation of the forms
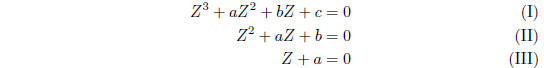
in which a, b c and d are fractions.
The impossibility of the last equation is clear because 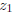 is not a fraction.
is not a fraction.
If it were a root of the first, then using long division to divide (I) by
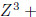
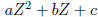 , we would find
, we would find
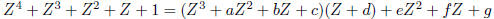
Substitute 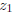 to find that
to find that 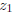 is also a root of
is also a root of
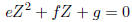
Then, as we just observed e is not 0, unless e = f = g =
0. If e is not 0,
divide by it. Thus either
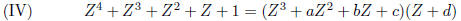
or  satisfies an equation of type (II). If it satisfies
(II), then perform a long
satisfies an equation of type (II). If it satisfies
(II), then perform a long
division to obtain
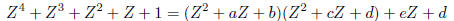
Since e + d cannot be 0 unless e = d = 0, we conclude
that
+ d cannot be 0 unless e = d = 0, we conclude
that
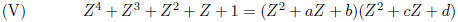
We now show that the factorizations of (IV) and (V) are
impossible. We
first observe a very important fact.
An equation of degree n
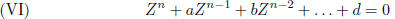
cannot have more than n roots!
Suppose (VI) has a root e. Using long division, divide by
Z − e. The
result is
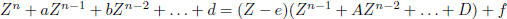
Substitute e to see that f = 0. Now any other root e' not
equal to e of (VI)
must be a root of
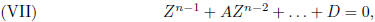
so that if (VI) had more than n roots, then (VII) would
have more than n−1.
All we have to do now is continue, working our way down to lower and lower
degree until we arrive at an equation of degree one
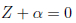
that clearly has only one root.


