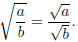Real Numbers, Exponents and Radicals
TED LAI
Section 1.2 Real Numbers
Definition. A real number r is a rational number if
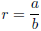where a and b are integers and b ≠ 0.
Some examples of rational numbers are: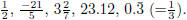 
Also
note
that each integer n is a rational number since
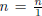, which is a fraction of two
integers.
Definition. A real number is an irrational number if it is not a rational
number.
Some examples of irrational numbers are: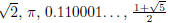 
(the golden
ratio).
Properties of Real Numbers. Let a, b, and c be real numbers. Then they
satisfy
the following properties:
Property 1 (The Commutative Property of Addition).
a + b = b + a
Property 2 (The Commutative Property of Multiplication).
a b = b a
Property 3 (The Associative Property of Addition).
(a + b) + c = a + (b + c)
Property 4 (The Associative Property of Multiplication).
(a b) c = a (b c)
Property 5 (The Distributive Property).
a (b + c) = a b + ac and (b + c) a = b a + ca
So, what’s the point of these trivial properties? Let’s illustrate their use by
an
example.
Example 1. Let x, y, z, and w be real numbers. Show (x+ y) (z +w) = x z
+y z +
x w + y w.
| (x + y) (z + w) | |
| = (x + y) z + (x + y) w | by Property 5 |
| = (x z + y z) + (x w + y w) | by Property 5 |
| = [(x z + y z) + x w] + y w | by Property 1 |
| = x z + y z + x w + y w |
Alternatively, one could verify the property numerically with explicit numbers,
but it would take forever to check all possible combinations of real numbers.
TED LAI
Properties of Fractions. Let a, b, c, d be real
numbers with b≠0 and d ≠ 0.
Then the following properties hold:
Property 6.
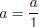
Property 7.
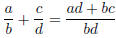
Property 8.
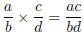
Property 9.
If c ≠ 0, then
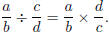
Sets and Intervals. Loosely speaking, a set is a
collection of objects. The objects
contained in a set are called elements of the set. A set could contain a finite
number
of elements or infinitely many elements.
Notation. Let S be a set. a∈ S denotes that a is an element of S.
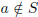denotes
that a is not an element of S.
Definition. Let S and A be sets. If every element contained in A is also
contained
in S, then A is a subset of S.
Sets frequently seen in class:
| Notation | Description |
| R Q Z R2 |
the set of all real numbers the set of all rational numbers the set of all integers the set of all ordered pairs of real numbers |
Notation. Let S and A be sets. A
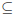S denotes that A is a
subset of S.
We say two sets A and B are equal if A 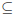B and B 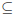A.
Notation.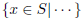 
denotes the set of all x in S such
that . . .
Invervals are subsets of R (see table above), and they correspond to line
segments
on the real number line. There are 9 types of intervals. Each one is represented
in
interval notation below.
Let a and b be real numbers such that a≤ b.
| Notation | Set Description |
 |
 |
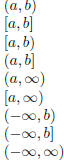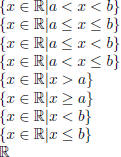| (see pg 15 in textbook for graphs) | |
CHAPTER 1 NOTES
Section 1.3 Exponents and Radicals
Integer Exponents.
Notation. If a is a real number and n is a positive integer, then the nth power
of a
is
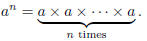
Observe that for any real number a and any positive integers m and n,
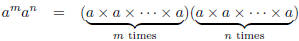
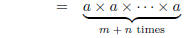by Property 4 in
Section 1.2
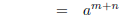
Also one could show that
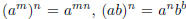for any real number b, and
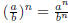for any nonzero real number b.
Radicals.
Definition. Let a be a real number such that a ≥0. A square root of a is
a number
b such that b2 = a.
It can be shown that every positive number has exactly two distinct square
roots:
a positive one and a negative one. For example, 2 and -2 are both square roots
of
4 since 22 = 2 × 2 = 4 and (−2)2 = (−2) × (−2) = 4.
Notation. Let a be a real number such that a ≥0. If a is positive,
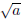denotes the positive square root of a. If a
= 0, then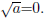 
Properties of Square Roots. Let a, b be real numbers with a≥ 0 and b≥ 0.
Then the following properties hold:
Property 10.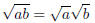
Property 11.If b ≠ 0, then