Try the Free Math Solver or Scroll down to Tutorials!

Enter expression, e.g. (x^2-y^2)/(x-y)

Enter expression, e.g. x^2+5x+6

Enter expression, e.g. (x+1)^3

Enter a set of expressions, e.g. ab^2,a^2b

Enter equation to solve, e.g. 2x+3=4

Enter equation to graph, e.g. y=3x^2-1

Depdendent Variable

Number of equations to solve:

Equ. #1:

Equ. #2:

Equ. #3:

Equ. #4:

Equ. #5:

Equ. #6:

Equ. #7:

Equ. #8:

Equ. #9:

Solve for:

Enter inequality to solve, e.g. 2x+3>4

Enter inequality to graph, e.g. y<3x^2-1

Dependent Variable

Number of inequalities to solve:

Ineq. #1:

Ineq. #2:

Ineq. #3:

Ineq. #4:

Ineq. #5:

Ineq. #6:

Ineq. #7:

Ineq. #8:

Ineq. #9:

Solve for:

Math solver on your site

Please use this form if you would like
to have this math solver on your website,
free of charge.

Name:

Email:

Your Website:

Msg:

Other Miscellaneous Problems

95. Prove that 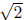is irrational. In other words, prove that if r is a rational number then r^2 ≠

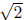
96. Let m be an integer. Prove that if m^2 is odd, then m is odd.

97. Let x be an integer. Prove that if x^2 is not divisible by 4 then x is odd.

98. Let x and y be integers. Prove that if xy is even then either x is even or y is even.

99. Let x and y be integers. Prove that if xy is odd then both x and y are odd.

100. Let x be an integer. Prove that if 8 does not divide x^2 − 1 then x is even.

101. Let x, y and z be integers. Prove that is x does not divide yz then x does not divide z.

102. Let a and b be integers. Prove that if ab is odd, then both a and b are odd.

103. Let a and b be integers. Prove that if a − b is odd then a + b is odd.

104. Prove that there exist integers m and n so that 2m + 7n = 1.

105. Prove that there do not exist integers m and n so that 2m + 4n = 7.

106. Let a, b, and c be integers. Prove that if a divides b − 1 and a divides c − 1 then a divides bc − 1.

Your Math Help is on the Way!

More Math Help

Other Miscellaneous Problems