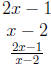Try the Free Math Solver or Scroll down to Tutorials!

Enter expression, e.g. (x^2-y^2)/(x-y)

Enter expression, e.g. x^2+5x+6

Enter expression, e.g. (x+1)^3

Enter a set of expressions, e.g. ab^2,a^2b

Enter equation to solve, e.g. 2x+3=4

Enter equation to graph, e.g. y=3x^2-1

Depdendent Variable

Number of equations to solve:

Equ. #1:

Equ. #2:

Equ. #3:

Equ. #4:

Equ. #5:

Equ. #6:

Equ. #7:

Equ. #8:

Equ. #9:

Solve for:

Enter inequality to solve, e.g. 2x+3>4

Enter inequality to graph, e.g. y<3x^2-1

Dependent Variable

Number of inequalities to solve:

Ineq. #1:

Ineq. #2:

Ineq. #3:

Ineq. #4:

Ineq. #5:

Ineq. #6:

Ineq. #7:

Ineq. #8:

Ineq. #9:

Solve for:

Math solver on your site

Please use this form if you would like
to have this math solver on your website,
free of charge.

Name:

Email:

Your Website:

Msg:

Solving Inequalities with Logarithms and Exponents

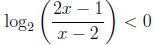
Let's start by seeing which x can even be put into the logarithm function in the
inequality. Since the domain of a logarithm function is (0,∞), we need

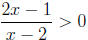
We know the fraction will be positive when both the numerator and denominator are
the same sign. To see when each piece changes sign, we look for when each piece is
0. The numerator: 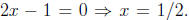The denominator:
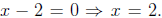
We now divide up the real line into intervals divided by these numbers x = 1/2, 2, and
check the sign of the numerator and denominator in each interval.

Interval

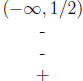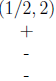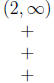So the domain of 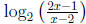is 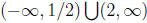. Note we do not include the end-
points (why?).

Now lets go on to solve the inequality. We first exponentiate both sides with base 2
(since this is the inverse operation of logarithm base 2).

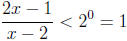
The next step in isolating x is to multiply by both sides by x - 2. Since multiplying
by a negative number reverses an inequality, we need to be careful about the sign
of x - 2, since that will affect the direction of the inequality. Let's first say
x > 2, so x - 2 > 0 and the direction of the inequality doesn't change, and we get

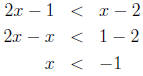
Well this violates our assumption that x > 2, so this tells us (2,∞) is not part of
our solution set. Next say x < 2, so x-2 is negative, and when we multiply by this
we need to switch the sign of the inequality:

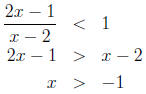
So we have that x > -1 and our assumption here was x < 2, giving us x is in
(-1, 2). But now we need to go back and check the domain of the logarithm function,
and see if any values in (-1, 2) are not in the domain. The domain we found is
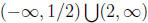, so we see that [1/2, 2) needs to be removed from (-1, 2), leaving
only (-1, 1/2).

To illustrate this point, take x = 1. This satisfies the inequality 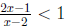, but 1 is not
in the domain of our original logarithm function and cannot be put into our original
inequality.

So the final answer - the solution set to the inequality is (-1, 1/2), or -1 < x < 1/2.

2.

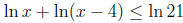
Again we'll first check the domain. ln x gives us the domain restriction x > 0, and
ln(x-4) gives us the domain restriction x > 4. Since a number > 4 is > 0, our domain
is x > 4.

Now we'll solve the inequality, first using properties of logs and then exponentiating
both side (with base e):

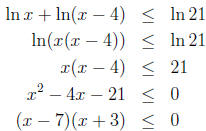
The product (x - 7)(x + 3) will be less than 0 when the factors have opposite sign.
You can set up a similar table as in the first problem, and we see that the factors are
opposite sign when -3 < x < 7. Now since the inequality is ≤, not a strict <, we
include the endpoints -3 and 7 (since the left side is allowed to actually = 0).

Now checking the domain, we found x > 4, so the actual solution set reduces from
[-3, 7] to (4, 7]. Notice 4 is not included, since it is not in the domain of ln(x - 4).
So the final answer - the solution set to the inequality is (4, 7], or 4 < x ≤7.

Your Math Help is on the Way!

More Math Help

Solving Inequalities with Logarithms and Exponents