General linear equations

Linear mapping = linear transformation = linear function

Definition. Given vector spaces V₁ and V₂, a
mapping L : V₁ → V₂ is linear if

L(x + y) = L(x) + L(y),
L(rx) = rL(x)

for any x, y ∈ V₁ and r ∈ R.

Basic properties of linear mappings:
• L(r₁v₁ + · · · + r_kv_k) = r₁L(v₁) + · · · + r_kL(v_k)
for all k ≥ 1, v₁, . . . , v_k ∈ V₁, and r₁, . . . , r_k ∈ R.
• L(0₁) = 0₂, where 0₁ and 0₂ are zero vectors in
V₁ and V₂, respectively.
• L(−v) = −L(v) for any v ∈ V₁.

Range and kernel
Let V,W be vector spaces and L : V → W be a
linear mapping.
Definition. The range (or image) of L is the set
of all vectors w ∈ W such that w = L(v) for some
v ∈ V. The range of L is denoted L(V).
The kernel of L, denoted ker L, is the set of all
vectors v ∈ V such that L(v) = 0.
Theorem (i) The range of L is a subspace of W.
(ii) The kernel of L is a subspace of V.

General linear equations
Definition. A linear equation is an equation of the form
L(x) = b,
where L : V → W is a linear mapping, b is a given vector
from W, and x is an unknown vector from V.
The range of L is the set of all vectors b ∈ W such that the
equation L(x) = b has a solution.
The kernel of L is the solution set of the homogeneous linear
equation L(x) = 0.
Theorem If the linear equation L(x) = b is solvable then the
general solution is
x₀ + t₁v₁ + · · · + t_kv_k ,
where x₀ is a particular solution, v₁, . . . , v_k is a basis for the
kernel of L, and t₁, . . . , t_k are arbitrary scalars.

Example.



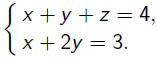
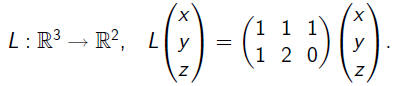
Linear equation: L(x) = b, where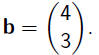

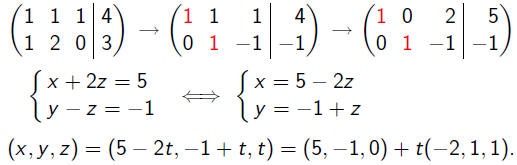
Example.
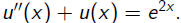
Linear operator L :
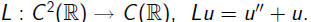
Linear equation: Lu = b, where b(x) = e^2x .
It can be shown that the range of L is the entire
space C(R) while the kernel of L is spanned by the
functions sin x and cos x.
Observe that

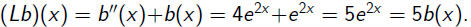
By linearity, 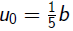is a particular solution.
Thus the general solution is

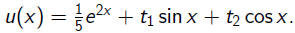
Matrix transformations
Any m×n matrix A gives rise to a transformation
L : Rⁿ → R^m given by L(x) = Ax, where x ∈ Rⁿ
and L(x) ∈ R^m are regarded as column vectors.
This transformation is linear.

Indeed, L(x + y) = A(x + y) = Ax + Ay = L(x) + L(y),
L(rx) = A(rx) = r (Ax) = rL(x).
Example.

Let e₁ = (1, 0, 0), e₂ = (0, 1, 0), e₃ = (0, 0, 1) be the
standard basis for R³. We have that L(e1) = (1, 3, 0),
L(e₂) = (0, 4, 5), L(e₃) = (2, 7, 8). Thus L(e₁), L(e₂), L(e₃)
are columns of the matrix.

Problem. Find a linear mapping L : R³ → R²
such that L(e₁) = (1, 1), L(e₂) = (0,−2),
L(e₂) = (3, 0), where e₁, e₂, e₃ is the standard
basis for R³.

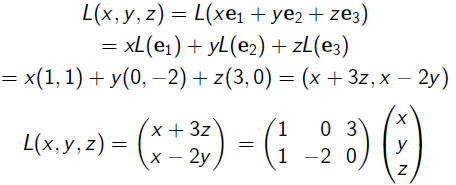
Columns of the matrix are vectors L(e₁), L(e₂), L(e₃).

Theorem Suppose L : Rⁿ → R^m is a linear map. Then
there exists an m×n matrix A such that L(x) = Ax for all
x ∈ Rⁿ. Columns of A are vectors L(e₁), L(e₂), . . . , L(e_n),
where e₁, e₂, . . . , e_n is the standard basis for Rⁿ.

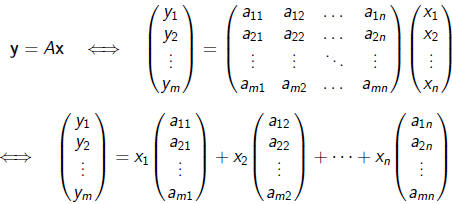
Linear transformations of R²
Any linear mapping f : R² → R² is represented as
multiplication of a 2-dimensional column vector by a
2×2 matrix: f (x) = Ax or

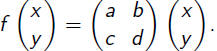
Linear transformations corresponding to particular
matrices can have various geometric properties.

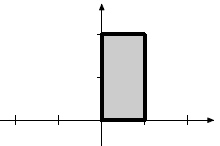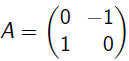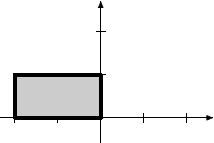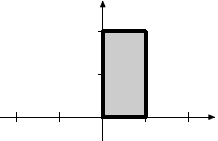
	Rotation by 90o

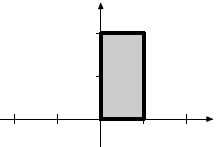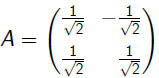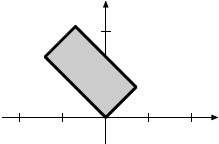	Rotation by 45o

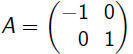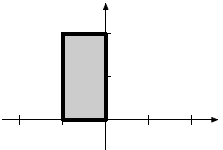	Reflection in the vertical axis

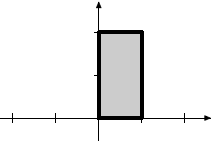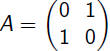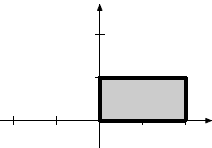	Reflection in the line x − y = 0

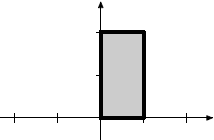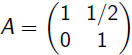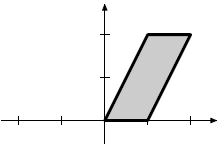	Horizontal shear

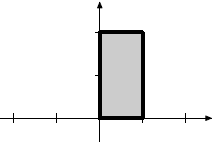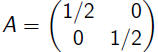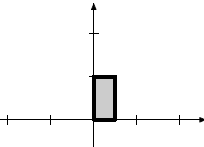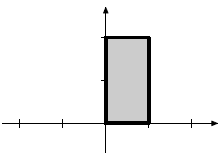
	Scaling

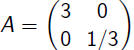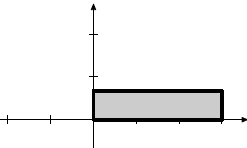	Squeeze

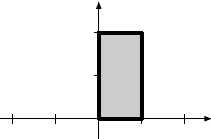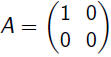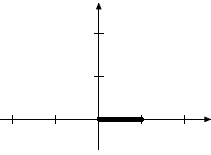	Vertical projection on the horizontal axis

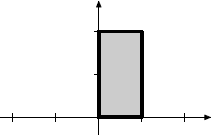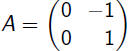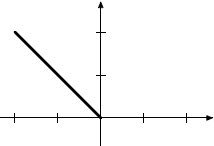	Horizontal projection on the line x + y = 0

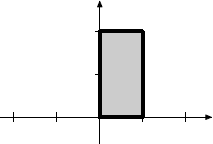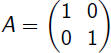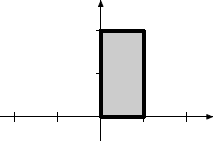	Identity