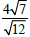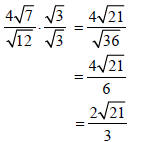Radical Expressions and Equations
Study Strategy –Note Taking
•Choosing a Seat
•Note-Taking Speed
•Things to Include
•Being an Active Learner
•Formatting Your Notes
•Rewriting Your Notes
•Write Down Each Step
Section 8.1–Square Roots and Radical Notation
Concept –Radical Expressions, Square Roots
The principal square root of b, denoted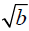 
,
is the positive number a such that a2 =b
The expression is called a radical
expression.
The sign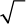 
is called a radical sign.
The expression contained inside the
radical sign is called the radicand.
Example –Radical Expressions, Square Roots
Simplify: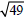
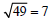because 72
=49
Example –Radical Expressions, Square Roots
Simplify, assume x is nonnegative: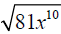
.
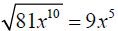because
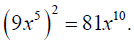
Concept –Product Property of Radicals
For any index n>1and any nonnegative
numbers a and b,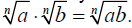
Example –Product Property of Radicals
Simplify: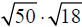
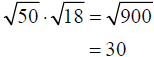
Example –Product Property of Radicals
Simplify: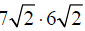
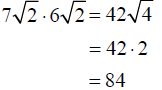
Concept –Quotient Property of Radicals
For any index n>1and any nonnegative
number a and positive number b ,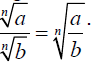
Example –Quotient Property of Radicals
Simplify: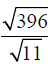
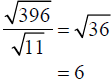
Section 8.2 -Simplifying, Adding, & Subtracting Radical Expressions
Concept –Simplifying Radicals
1. Completely factor the radicand.
2. Rewrite each factor as a product of two
factors. The exponent for the first factor should
be the largest multiple of the radical’s index that
is less than or equal to the factor’s original
exponent.
3. Use the product property to remove factors
from the radicand.
Example –Simplifying Radicals
Simplify: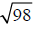
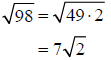
Concept –Like Radicals
Two radical expressions are called like
radicals if they have the same index and
the same radicand.
Example –Like Radicals
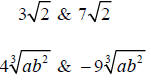
Concept –Adding and Subtracting Radical Expressions
1. Simplify each radical completely.
2. Combine like radicals by adding/subtracting
the factors in front of the radicals.
Example –Adding and Subtracting Radical Expressions
Subtract: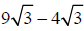
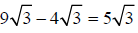
Example –Adding and Subtracting Radical Expressions
Add: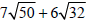
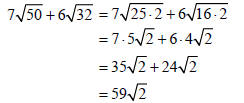
Section 8.3 –Multiplying and Dividing Radical Expressions
Concept –Multiplying Radical Expressions
If the index of each radical is the same,
multiply factors in front of the radical by
each other, and multiply the radicands by
each other. Simplify the resulting radical if
possible.
Example –Multiplying Radical Expressions
Multiply: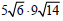
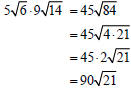
Concept –Multiplying Radical Expressions
If one or more of the expressions contains at
least two terms, multiply by using the
distributive property.
Example –Multiplying Radical Expressions
Multiply: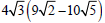
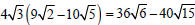
Example –Multiplying Radical Expressions
Multiply: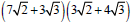
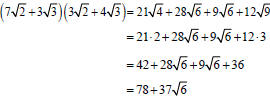
Concept -Multiplying Radical Expressions
To square a radical expression containing two or more terms, multiply the
expression by itself.
Example -Multiplying Radical Expressions
Multiply: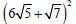
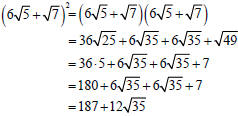
Concept –Rationalizing a Denominator with Only
One Term Containing a Radical with an Index of n
1. Multiply both the numerator and denominator
by a radical expression that results in the
radicand being a perfect nth power.
2. Simplify the radical in the denominator.
3. Simplify the fraction by dividing out factors
that are common to the numerator and
denominator, if possible.
Example -Rationalizing a Denominator with Only
One Term Containing a Radical with an Index of n
Rationalize the denominator:
