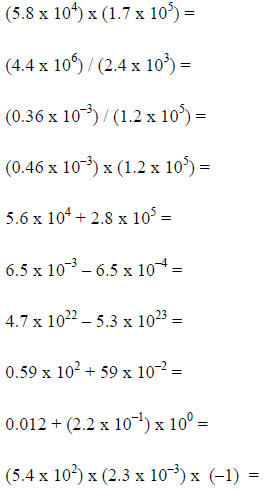Powers of Ten and Calculations
Power of ten is the mathematical shorthand for writing
very large or very small numbers, using positive
or negative exponents of base 10. The exponent is written as a superscript
numeral to the right of the 10.
The Basics:
(1) Ten with a positive exponent means to multiply 10 by itself the number of
times indicated by the
power. For example, 103 = 10 x 10 x 10 = 1000.
(2) Ten to a negative power means to multiply 0.1 (1/10) by itself the number of
times indicated by
the power. For example, 10-3 = 0.1 x 0.1 x 0.1 = 0.001 (equivalent to 1/1000, or
the reciprocal of
103, which is 10-3).
(3) Ten to the zero power (100) equals 1, by definition. Zero (0) can only be
represented by itself.
(4) Any number can be expressed as a power of ten by using a scalar value and an
exponent. For
example, 212 = 2.12 x 100 = 2.12 x 102 and 0.0098 = 9.8 x 10-3.
(5) When multiplying two numbers expressed as powers of ten, add the exponents.
For example,
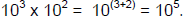
(6) When dividing two numbers expressed as powers of ten, subtract the
exponents. For example,
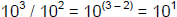 and
and 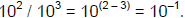
(7) When multiplying or dividing numbers in scientific notation, multiply (or
divide) the scalar
values separately from the exponents, then combine the two.
For example,
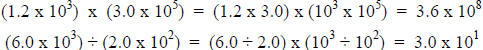
(8) When adding or subtracting numbers expressed in powers of ten, transform the
values to a
common exponent, then add or subtract the scalar (non-exponent) values. For
example, 3.8 x 103
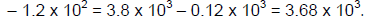
To make thinking in large and small numbers a little easier, scientists and
engineers commonly
express powers of ten in multiples of 3 (or –3), which is equivalent to
counting, 1 thousand, 1 million, 1
billion, 1 trillion, and so on. In computer lingo, this idea is expressed by the
prefixes kilo-, mega-, giga-,
and tera-, as in “megabytes.”
 |
Equivalent value |  |
Equivalent value |
 |
|||
Other things to keep in mind about math with exponents:
Use a leading zero in the ones place for any decimal
values
for example, 0.025 instead of .025
When using scientific notation, express the scalar value with a numeral in the
ones place
for example, 1.25 x 105 instead of 0.0125 x 107.
The exception to the above guideline is when you need to use a common exponent
for
operations such as addition and subtraction;
for example, 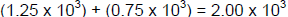
instead of 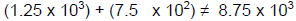
Be careful about moving the decimal point and the exponent in the correct
direction
(especially for negative exponents). In your mind (or on paper),
convert the number
expressed in scientific notation into a decimal value, and
ask yourself whether the
exponent gets larger or smaller. (Admittedly, this can
be tricky.)
For example,
0.254 x 102 (0.254 x 100 = 25.4) becomes 2.54 x 101, NOT 2.54 x 103 (which is
2540)
and
25.4 x 102 (25.4 x 100 = 2540) becomes 2.54 x 103, NOT 2.54 x 101 (which is
25.4)
Likewise,
0.15 is equivalent to 1.5 x 10-1 or 0.015 x 101 (moving the decimal point either
way)
A rule of thumb for decimal places and exponents:
For positive exponents, 1 x 10n n is equal to the number of zeroes to the right
of 1.
Examples: 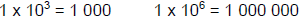
For negative exponents, 1 x 10-n there are (n-1) zeroes to the left of 1
(i.e., the equivalent decimal position would be to the right of the 1)
Examples: 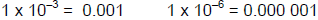
Remember the relationship between positive and negative exponents and
reciprocals of
fractions:
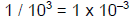 and
and 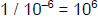
AND, when adding or subtracting with scientific notation, always remember to
convert to
a common exponent:
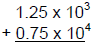 |
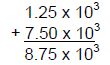 |
which is equivalent to  |
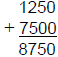 |
|
| convert | ||||
to |
Express each number as a power of ten:
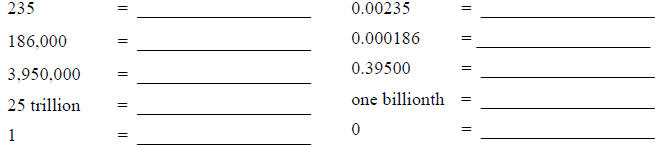
(can zero be represented as a power of ten?)
Express each as a non-“power of ten” number:
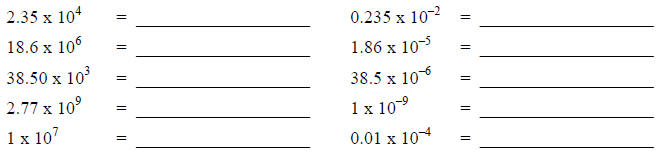
Complete each calculation, show intermediate steps when
appropriate, and express the
answer as a power of ten: